XIII - XVI ora
Si sono visti criteri sufficienti perché un sottogruppo N di G sia normale. Si è introdotto il gruppo quoziente G/N e si è visto l’esempio di Z/nZ.
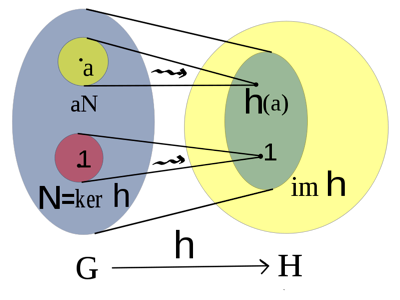
Si è definito il nucleo di un omomorfismo di gruppi e si è dimostrato il teorema fondamentale di omomorfismo per gruppi, presentando alcuni esempi di applicazione del teorema.
Si sono infine date le definizioni di anello e di anello unitario presentandone alcuni esempi e proprietà.
Si consiglia di svolgere entro la prossima lezione gli esercizi elencati nel file Esercizi110330.pdf

Lezioni del 29 e 30 marzo 2011
mercoledì 30 marzo 2011