Appunti per il corso di Geometria I
Giorgio Ottaviani
Chiudere ogni finestra che che viene aperta prima di aprirne un'altra!
Questi appunti sono in costruzione, ogni commento è benvenuto! (spedire una mail a ottaviani@math.unifi.it)
- Il linguaggio delle funzioni
- Lo spazio Rn
- Le matrici
- L'algoritmo di Gauss ed i sistemi lineari
- Spazi vettoriali e funzioni lineari
- Basi ortonormali e spazi ortogonali
-
Complementi: somma e somma diretta, la formula di Grassmann
- Il determinante
- Autovalori e autovettori. Il teorema spettrale.
0. Il linguaggio delle funzioni
Scriveremo una funzione da un insieme A ad un insieme B con la notazione f : A ® B.
Per ogni a Î A l'elemento f(a) Î B si dice l'immagine di a
tramite f. Due funzioni f1, f2 da A a B sono uguali (f1 =
f2) quando f1(a) = f2(a)
"a Î A. Date due funzioni ¦ : A ® B e
g : B ® C,la composizione g · f :
A ® C è definita da
(g · f )(a) : =
g[¦(a )].
La funzione identità 1
A : A ®A è definita dalla formula 1A( a )
:= a "a Î A. È utile pensare alle funzioni come
algoritmi (ma a livello fondazionale è pericoloso!) dove gli elementi di A corrispondono all'input ed elementi di B corrispondono all'output. La funzione identità corrisponde allora all'algoritmo che lascia invariato ogni elemento in input.
Esercizio 0.1 Se ¦ : A ® B provare che 1B·¦=¦, ¦·1A=¦. Soluzione
Se ¦ : A ® A.allora la composizione f ·f si indica con f 2. Analogamente f k indica la composizione di f con se stessa per k volte.
Esempio 0.2 Se
¦ : Z ® Z è definita da f(x)
:= 2x allora f
k(x)=2
kx
" x
Î Z "k
Î N Prop. 0.3 Consideriamo tre funzioni
f:A
® B
g:B
® C
h:C
® D.
Allora (h
· g)
· f=h
· (g
· f), cioè la composizione tra funzioni gode della proprietà associativa.
Dimostrazione Definizione f:A
® B si dice
iniettiva se per ogni a, a'
Î A tali che f(a)=f(a') abbiamo a=a'.
Definizione f:A
® B si dice
suriettiva se per ogni b
Î B esiste a
Î A tale che f(a)=b.
Osservazione 0.4 Siano f,g :
Z ® Z definite da f(x)=|x|
, g(x)=2x. Allora f · g(2)=2 , g
· f(2)=-2 , quindi f· g ¹ g
· f. (Segue che la composizione tra funzioni non è commutativa.) Questo fatto sarà particolarmente
importante riguardo alle trasformazioni geometriche del piano e dello spazio.
Esercizi di base sulle funzioni iniettive e suriettive.
Esercizi avanzati sulle funzioni iniettive e suriettive.
Definizione Una funzione f si dice biunivoca se
è iniettiva e
suriettiva.
Esercizi sulle funzioni biunivoche. Se f è biunivoca allora per ogni b Î B esiste unico a Î A tale che f(a)=b. L'esistenza di a è garantita dalla suriettività di f, l'unicità di a è garantita dall'iniettività di f .
Esempio 0.5 Sia g : Z ® Z definita da g(x)=2x e f : Z ® Z definita da f(x)=[x/2] dove [ ] denota la parte intera.
Allora f· g =1 Z, mentre g· f(x) è uguale a x se x è e pari ed è uguale a x-1 se x è dispari. Definizione Una funzione f : A® B si dice invertibile se esiste una funzione g : B® A tale che f· g =1 B, g· f =1 A
Lemma-Definizione 0.6 Nella definizione di invertibilità di f, se g esiste allora è unica, si chiama inversa di f e si indica con la notazione g=f -1. Dimostrazione
Teorema 0.7 Sia f : A® B . f è invertibile Û f è biunivoca
Dimostrazione
Þ Per ipotesi esiste f -1 inversa di f. Proviamo che f è iniettiva. Se f(a)=f(a') allora f -1 · f(a)=f -1 ·f(a') cioè a=a', quindi f è iniettiva. Proviamo che f è suriettiva. Se bÎ B allora f[f -1(b)]=b quindi f è suriettiva.
Ü Per ipotesi per ogni b Î B esiste unico a
Î A tale che f(a)=b. Definiamo quindi
f -1(b)=a.
È immediato verificare che f -1 è l'inversa di f.
Esercizi (non facili) per la comprensione dell'equivalenza tra funzioni biunivoche
e funzioni invertibili.
Per ogni insieme S denotiamo con T(S) l'insieme delle
funzioni biunivoche da S in se stesso. Ai fini del presente corso ci
interesserà soprattutto il caso in cui S è lo spazio
(affine o euclideo). T(S) ammette l'operazione di composizione.
Rispetto a questa operazione sono verificate le seguenti tre
proprietà
- Per ogni f, g, h Î T(S) vale (f·g)·h= f· (g·h) proprietà associativa
- Per ogni f Î T(S) vale 1S· f= f·1S =f esistenza dell'elemento neutro
- Per ogni f Î T(S) esiste f -1Î T(S) tale che f -1· f= f·f -1= 1S esistenza dell'inverso
Le tre proprietà precedenti ci permettono di affermare che T(S) è un gruppo
Un sottoinsieme non vuoto A di T(S) è un
sottogruppo se - per ogni f Î
A allora f -1Î A A è chiuso rispetto all'inverso
- per ogni f,g Î A allora f·g Î A A è chiuso rispetto alla composizione
Notiamo che ogni sottogruppo è in particolare un gruppo, cioè soddisfa gli assiomi di gruppo.
Se S è il piano euclideo allora le isometrie, le traslazioni, le similitudini formano sottogruppi significativi di T(S).
I gruppi sono insiemi "arricchiti" dall'operazione (la composizione nel caso di T(S) ). Un insieme con operazioni che soddisfano certe proprietà si dice in generale una struttura algebrica. I gruppi sono tra le strutture algebriche più importanti. Altri esempi che vedremo più avanti sono gli spazi vettoriali. Le funzioni tra gruppi che si comportano "bene" rispetto all'operazione prendono il nome di omomorfismi tra gruppi.
Esempi Sia S il piano euclideo. Denotiamo con d(P,Q) la distanza di due punti P, Q Î S. Una funzione f Î T(S) si dice una isometria se d(P,Q)=d(f(P),f(Q)), cioè se conserva la distanza. Il sottogruppo di T(S) che consiste nelle isometrie che portano un triangolo equilatero in se stesso è formato da 6 elementi (3 simmetrie assiali, e le tre rotazioni attorno al baricentro di angoli risp. 0, 2p/3, 4p/3). La rotazione di un angolo 0 coincide con l'identità.
Il sottogruppo di T(S) che consiste nelle isometrie che portano un poligono regolare di n lati in se stesso è formato da 2n elementi.
Il sottogruppo di T(S) che consiste nelle isometrie che portano un cerchio in se stesso è formato da infiniti elementi. Rn è per definizione il prodotto cartesiano di R con se stesso per n volte, cioè gli elementi di Rn sono n-ple di numeri reali che scriveremo con la notazione
x =(x1,..., xn) ÎRn Chiameremo gli elementi di Rn vettori con n componenti. Ad esempio (2,4,3)ÎR3 è un vettore con 3 componenti. Gli elementi xi per i=1,...,n si dicono le componenti di x.
2 è la prima componente di (2,4,3), 4 è la seconda componente di (2,4,3) e così via.
È ben noto che gli elementi di R2 si possono identificare con i punti di un piano, gli elementi di R3 con i punti dello spazio. Vedremo che gli elementi di Rn si possono identificare con i punti di uno spazio a n dimensioni.
Se x =(x1,..., xn) , y =(y1,..., yn) ÎRn è definita la somma
x+y =(x1+y1,..., xn+ yn) ÎRn La somma è quindi definita componente per componente. Denotiamo con 0=(0,...,0) la n-pla costituita da tutti le componenti nulle. Per ogni x =(x1,..., xn) ÎRn denotiamo con -x =(-x1,..., -xn) ÎRn la n-pla costituita da tutti le componenti di x cambiate di segno.
La somma soddisfa alle tre proprietà di facile verifica - Per ogni x, y, z Î Rn vale
(x+ y)+z=x+(y+z) proprietà associativa - Per ogni x Î Rn vale
0+x= x+0 =x esistenza dell'elemento neutro - Per ogni x Î Rn esiste -xÎ Rn tale che
-x+x=x+(-x)=0 esistenza dell'inverso (opposto)
Le tre proprietà precedenti sono analoghe a quelle viste per T(S) con la differenza che l'operazione è denotata con il simbolo + (notazione additiva), l'elemento neutro con 0 e l'inverso con -x (invece che con x -1 ). Le tre proprietà ci permettono di affermare che Rn è un gruppo
Vale in questo caso una quarta proprietà - Per ogni x, y Î Rn vale
x+y=y+x proprietà commutativa
Queste quattro proprietà ci permettono di affermare che Rn è un gruppo abeliano (o commutativo).
T(S) in generale non è abeliano.
Su Rn si può definire una seconda operazione, di natura un pò diversa perché non è un'operazione interna all'insieme, cioè non si esegue tra due elementi di Rn.
Consideriamo x =(x1,..., xn) ÎRn e l ÎR. Il prodotto l xÎ Rn è definito da l x= (l x1,..., l xn) Ad esempio
5(2,4,3)=(10,20,15)
l x prende il nome di prodotto di x per lo scalare l . Le proprietà delll'operazione di prodotto per uno scalare sono le seguenti, di facile verifica - Per ogni x Î Rn, per ogni l, m Î R vale
(l+m)x= lx +mx proprietà distributiva degli scalari - Per ogni x, y, Î Rn, per ogni l Î R vale
l(x+y)= lx +ly proprietà distributiva dei vettori - Per ogni x Î Rn, per ogni l, m Î R vale
(lm)x= l( mx) - Per ogni x Î Rn vale
1x=x
Le otto proprietà precedenti ci permettono di affermare che Rn è uno spazio vettoriale
Le seguenti proprietà sono di immediata verifica e sono conseguenza delle otto precedenti, cioè valgono in ogni spazio vettoriale. I vettori applicati nell'origine e l'interpretazione geometrica delle operazioni.
Ogni vettore x Î Rn può essere interpretato geometricamente come un segmento orientato con punto iniziale l'origine e punto finale x stesso. I segmenti orientati si disegnano come delle freccette e questa è la rappresentazione che si dà usualmente dei vettori. Questa descrizione è ben nota dalla Fisica, dove si sottolinea che un vettore è descritto da tre grandezze: la direzione, il verso e la lunghezza. La somma tra vettori si può calcolare geometricamente con la regola del parallelogramma, cioè x+y corrisponde alla diagonale con punto iniziale l'origine del parallelogramma che ha per lati x e y. Il prodotto lx corrisponde al vettore che ha la stessa direzione di x , stesso verso se l>0 oppure verso opposto se l<0 e lunghezza ottenuta moltiplicando la lunghezza di x per |l|. La lunghezza di un vettore di Rn .
Se x Î Rn la sua lunghezza (euclidea) è per definizione |x|:= 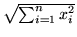
La formula precedente usa il simbolo di sommatoria.
Per n=2 la formula precedente si giustifica attraverso il teorema di Pitagora. Infatti il segmento che unisce l'origine con (x1,x2) è l'ipotenusa di un triangolo rettangolo i cui cateti misurano rispettivamente |x1| e |x2|. Notiamo che - |x| ³0 per ogni x Î Rn
- |x| =0 se e solo se x=0
Le proprietà precedenti sono di verifica immediata. Vale una terza proprietà, detta disuguaglianza triangolare, che dimostreremo tra breve, come conseguenza della disuguaglianza di Cauchy-Schwarz. - |x+y| £ |x|+|y| per ogni x, y Î Rn
disuguaglianza triangolare
Angolo tra due vettori in R2 .
Prop. 1.1 Siano v=(v1, v2) e w=(w1, w2) due vettori (applicati nell'origine) di lunghezza 1 in R2 che formano un angolo q. Allora
cos q= v1w1+ v2w2
Dimostrazione Sia a l'angolo che v forma con l'asse delle ascisse. Allora v=(v1, v2)=(cos a, sen a )
Quest'ultima uguaglianza tra vettori (uguaglianza vettoriale) equivale alle due uguaglianze
v1 = cos a, v2 = sen a.
Vale anche
w=(w1, w2)=(cos (a+q), sen (a+q) )
Dalla formula di sottrazione
cos q=cos [(a+q)-a]= cos( a+q)cosa+ sen( a+q)sena =
= w1v1+ w2v2
Teorema 1.2 Siano v=(v1, v2) e w=(w1, w2) due vettori non nulli (applicati nell'origine) in R2 che formano un angolo q. Allora
cos q= (v1w1+ v2w2)/(|v| |w|)
Dimostrazione L'angolo tra v e w è lo stesso dell'angolo tra i loro normalizzati
(1/|v|)v=( v1/ [Ö v12+v22], v2/ [Ö v12+v22] )
e
(1/|w|)w=( w1/ [Ö w12+w22], w2/ [Ö w12+w22] )
La formula segue allora dalla prop. precedente. Il prodotto scalare in R2 .
Le formule trovate per gli angoli suggeriscono di porre la seguente definizione
Definizione 1.3 Dati due vettori v=(v1, v2) e w=(w1, w2) in R2 definiamo v. w:= v1w1+ v2w2 che si dice prodotto scalare di v e w.
È importante osservare che v.v= v12+ v22=|v|2 Pertanto il teorema 1.2 può essere così riformulato
Teorema 1.2 (riformulazione)
Siano v e w due vettori (applicati nell'origine) in R2 che formano un angolo
q. Allora
cos q=
(v.w) /(|v| |w|)
È utile scrivere la formula precedente nella forma
v.w=(|v| |w|)cos q
che vale anche nel
caso in cui v oppure w sono nulli.
Dalle formule precedenti segue che v e w sono ortogonali se e solo
se v.w= 0
Il prodotto scalare in
Rn .
La generalizzazione naturale del prodotto scalare a Rn è
la seguente
Definizione 1.4 Dati due vettori v=(v1,..., vn) e w=(w1,..., wn) in Rn definiamo v. w:= Si=1n viwi= v1w1+ ...+vnwn che si dice prodotto scalare di v e w.
Proprietà del prodotto scalare - v.w= w.v
simmetria
- ( lv1+ m v2)
.w= l (v1.w)+
m (v2.w) linearità rispetto alla prima
componente
- v.( lw1 +
m w2)= l (v. w1)
+ m (v. w2) linearità rispetto alla
seconda componente
Le verifiche delle proprietà precedenti seguono dalla definizione.
Osserviamo che vale anche
la formula
Lemma 1.5 v . v= |v|2
La disuguaglianza di Cauchy-Schwarz
Teorema 1.6 (Cauchy-Schwarz)
Per ogni v, w ÎRn vale |v.w|
£ |v| |w|
e vale l'uguaglianza se e solo se v e w hanno la stessa direzione.
Dimostrazione Se w=0 la disuguaglianza è vera. Supponiamo quindi che w sia non nullo e calcoliamo
per ogni t Î R 0 £ |v+tw|2= (v+tw) . (v+tw) = v. v+tv.w+ tw.v+t2w .w=
per la simmetria ed il lemma 1.5
=|v|2+2t v.w+ t2|w|2
L'espressione precedente è un polinomio di secondo grado in t con coefficiente di grado massimo positivo. Siccome il polinomio è sempre non negativo segue che il suo discriminante è non negativo (abbiamo una parabola con concavità verso l'alto sopra all'asse delle ascisse) da cui
(v.w)2-|v|2 |w|2 £ 0
che equivale alla tesi.
Quando la parabola tocca l'asse delle ascisse in un punto esiste un valore di t che annulla il polinomio, e questo accade nel caso limite in cui il discriminante è nullo. Per questo valore di t allora v+tw=0, cioè v=-tw, questo significa che v, w hanno la stessa direzione. Abbiamo |v+w|2=(v+w). (v+w)= |v|2+2 v. w+ |w|2 £
(per la disuguaglianza di Cauchy-Schwarz)
|v|2+2 |v| |w|+ |w|2 =(|v|+|w|)2 che equivale alla disuguaglianza triangolare. Vale l'uguaglianza esattamente quando vale l'uguaglianza nella disuguaglianza di Cauchy-Schwarz che abbiamo applicato (attenzione perchè non compare il valore assoluto, quindi v. w deve essere non negativo!). Questo conclude la dimostrazione.
Variazioni sul tema - |v-w| £ |v|+|w|
sostituendo -w al posto di w - | |v|-|w| | £|v+w|
infatti |v|=|(v+w)-w| £|v+w|+|w|
L'ultima disuguaglianza equivale al fatto geometrico che (la lunghezza di) un lato di un triangolo è maggiore o uguale della differenza degli altri due mentre la disuguaglianza triangolare equivale al fatto che (la lunghezza di) un lato è minore o uguale della somma degli altri due. Questa osservazione spiega l'origine dell'aggettivo "triangolare".
Una matrice mxn consiste di mn elementi aij
disposti in m righe ed in n colonne.
L'elemento aij
si dice di posto (i,j) e può essere visto come il j-esimo elemento della riga i-esima
oppure come il i-esimo elemento della colonna j-esima.
Le definizioni di somma e di prodotto per uno scalare
tra matrici sono analoghe a quelle viste per R n
e si applicano componente per componente.
Se A e B sono matrici mxn allora la somma A+B ha come elemento di posto (i,j)
l'elemento aij+bij, mentre se
c è un numero reale allora cA ha come elemento di posto (i,j)
l'elemento caij.
L'operazione di prodotto righe per colonne tra due matrici richiede invece un'attenzione
particolare. È possibile moltiplicare una matrice mxn A con una matrice nxp B
ed il risultato è una matrice mxp che indichiamo con AB. Se A è costituita dalle righe
A1...Am e B è costituita dalle colonne
B1...Bp allora l'elemento di posto (i,j) è
di AB è dato dal prodotto scalare AiBj, che si scrive in formula
come Sk=1maikbkj.
Sia ei il vettore (colonna) che ha tutte le componenti nulle tranne la
i-esima che è uguale a 1. Notiamo subito che per ogni vettore x nx1 vale
x=x1e1+...+xnen.
Se A è una matrice mxn allora Aej è la j-esima colonna di A.
Invece eit A è la i-esima riga di A (a patto di considerare
eit con m componenti.
Notiamo subito che il prodotto di due matrici quadrate nxn è ancora una matrice quadrata
nxn. La matrice identità I che ha tutti 1 sulla diagonale e tutti 0 al di fuori
è l'elemento neutro per questo prodotto. L'elemento di posto (i,j) della matrice
identità è uguale a 1 se i=j ed è uguale a 0 se i ¹ j,
si indica con dij e si chiama "simbolo di Kronecker".
Vale quindi AI=IA=A per ogni matrice quadrata nxn A.
Definizione Una matrice quadrata A si dice invertibile se esiste una matrice B
tale che AB=BA=I.
La matrice B, se esiste, si dice l'inversa di A e si indica con A-1.
Vedremo che la definizione precedente può
essere indebolita.
Una peculiarità del prodotto tra matrici è che esistono matrici non nulle che non sono invertibili.
Questo concetto risulterà più chiaro con la corrispondenza tra matrici e applicazioni lineari.
Esercizio Due matrici non nulle A e B si dicono divisori dello zero se AB=0. Trovare
due matrici 2x2 che sono divisori dello zero. Provare che un divisore dello zero non può
essere invertibile.
Sistemi lineari e scrittura matriciale
Un sistema lineare di m equazioni in n incognite ha la forma Ax=b
dove A è una matrice mxn
(che prende il nome di matrice del sistema), x=(x1,...,xn)
è il vettore colonna delle incognite e b=(b1,...,bm)
è il vettore colonna dei termini noti. Si noti che il prodotto righe per colonne
di A (mxn) con x (nx1) ha per risultato una matrice mx1.
Impareremo a risolvere completamente un sistema lineare. Questo vuol dire
sapere riconoscere se un sistema ha o meno soluzioni, ed in caso affermativo
saper calcolare tutte le soluzioni. L'insieme delle soluzioni di un sistema lineare
ha una struttura semplice, vedremo che è sempre un traslato di un sottospazio vettoriale.
Un sistema lineare si dice omogeneo quando b=0, cioè quando ha la forma Ax=0.
I sistemi lineari ammettono sempre la soluzione x=0.
EsercizioScrivere un sistema lineare che non ha soluzioni.
L'algoritmo di Gauss
Su una matrice possiamo eseguire le seguenti tre operazioni elementari su una matrice A.
- Operazione elementare di tipo I: scambia tra loro due righe di A, cioè Aj viene
sostituita da Ai e Ai viene sostituita da Aj .
- Operazione elementare di tipo II: moltiplica una riga data per uno scalare non nullo, cioè
Aj viene sostituita da cAj con c ¹0.
- Operazione elementare di tipo III: somma ad una riga un
scalare di un'altra, cioèsostituisce alla riga Aj la riga Aj+
lAi .
Mediante operazioni elementari di tipo I, III una qualunque matrice viene ricondotta ad una matrice a scalini.
La dimostrazione di questo fatto è costruttiva e può essere ottenuta
per induzione sul numero delle righe. Infatti
ogni matrice con una sola riga è a scalini. Adesso se A è
una matrice qualunque, consideriamo la
sua prima colonna non nulla. Con operazioni elementari di tipo I possiamo
trasformare A in una nuova matrice (che per abuso di notazione chiameremo ancora con A)
la cui prima colonna non nulla ha un elemento non nullo nella prima riga,
che chiamiamo a1i, questo è il primo pivot. Adesso con
operazioni elementari di tipo III si trasforma A in una nuova matrice dove sono nulli
tutti gli elementi sotto il pivot a1i, quindi la
prima colonna non nulla ha soltanto il primo elemento non nullo.
Consideriamo adesso la sottomatrice A'ottenuta
da A cancellando la prima riga e le prime i colonne.
Per ipotesi induttiva A' può essere trasformata in una matrice a scalini
conh operazioni elementari di tipo I e III. Queste operazioni permettono
di ridurre a scalini A stessa.
L'algoritmo che abbiamo appena descritto è la versione più semplice
di quello che oggi è noto come algoritmo di Gauss.
I pivot sono gli elementi che appaiono sulle estremità degli scalini
e sono sempre non nulli. Può darsi che i pivot siano in numero minore rispetto alle righe
perché le ultime righe della matrice potrebbero diventare identicamente nulle
e quindi non contenere pivot.
In particolare mediante operazioni elementari di tipo I, III una qualunque matrice quadrata viene ricondotta ad
una matrice a scalini che è triangolare. Se la matrice triangolare ha l'ultima riga diversa da zero allora
ha tutti gli elementi diagonali diversi da zero e mediante successive operazioni elementari di tipo I, III viene
ricondotta ad una matrice diagonale.
Le operazioni elementari di tipo II permettono di normalizzare tutti i pivot al valore 1.
Quindi mediante operazioni elementari di tipo I, II, III una qualunque matrice viene ricondotta ad una matrice
a scalini, dove i pivot valgono 1.
In particolare mediante operazioni elementari di tipo I, II, III
una qualunque matrice quadrata viene ricondotta ad una matrice triangolare dove sulla diagonale appaiono
soltanto 0,1.
L'algoritmo di Gauss si può applicare in particolare alle righe della matrice completa
(A|b)
di un sistema Ax=b. Ogni riga corrisponde ad una equazione.
Quindi le operazioni elementari di tipo I si corrispondono a scambi di posto tra diverse equazioni.
Le operazioni elementari di tipo II corrispondono alla moltiplicazione di
una equazione per una costante. Le operazioni elementari di tipo III corrispondono a sommare ad una
equazione un multiplo di un'altra (questo è noto talvolta come metodo di
"addizione e sottrazione" per risolvere un sistema).
È facile verificare che tutte le operazioni elementari sono invertibili
e non alterano le soluzioni di un sistema.
L'algoritmo di Gauss permette quindi di ricondurre un sistema ad un sistema a scalini
che ha le stesse soluzioni del sistema di partenza.
Questa operazione ` conveniente perchè i sistemi a scalini sono
facilmente risolubili. La risolubilità del sistema
è determinata dal seguente
Teorema (criterio di risolubilità per i sistemi lineari)
Il sistema Ax=b ammette almeno una soluzione se e solo se
riducendo a scalini la matrice (A|b) non si trovano pivot nella ultima colonna.
Dimostrazione (costruttiva)
Se c'è un pivot nell'ultima colonna, allora
l'ultima equazione non nulla si legge 0=1, che è impossibile.
Se invece ogni pivot è in una colonna precedente allora
il sistema si può sempre risolvere.
Infatti ogni variabile corrisponde ad una colonna della matrice
ed in una matrice a scalini le variabili sono divise in modo naturale in due gruppi:
quelle che corrispondono ai pivot (variabili dipendenti) e le altre (variabili libere).
L'ultima equazione contiene una sola variabile dipendente che può quindi essere espressa
in funzione delle variabili libere. Sostituendo questa espressione nella
penultima equazione si ricava che anche la penultima variabile dipendente
può essere espressa
in funzione delle variabili libere. Continuando in questo modo si ottiene che
tutte le variabili dipendenti possono essere espresse
in funzione delle variabili libere. Dando valori arbitrari alle variabili libere si ricavano quindi
soluzioni del sistema. Si trova in questo modo una parametrizzazione
dello spazio delle soluzioni del sistema.
Osserviamo dalla dimostrazione del teorema precedente
che l'algoritmo di Gauss permette di risolvere i sistemi lineari.
Il numero dei parametri da cui dipendono le soluzioni di un sistema è al numero delle variabili libere,
che è pari a numero delle incognite - numero dei pivot. Più avanti
daremo il nome di rango al numero dei pivot.
Sottospazi vettoriali
DefinizioneUn sottoinsieme non vuoto W di uno
spazio vettoriale V (in particolare di
Rn) si dice un sottospazio (vettoriale) se
- per ogni
l Î R e per ogni vÎ W si ha
l v Î W
- per ogni v, zÎ
W si ha v+z Î W
Le due condizioni precedenti possono essere riassunte
nella condizione - per ogni l, m Î R e
per ogni v, zÎ W si ha l v+m z
Î W
Proposizione Un sottospazio di uno spazio vettoriale contiene sempre l'origine.
Dimostrazione
Basta porre l =0 nella definizione di sottospazio. Se wÎ
W allora 0w=0Î W.
Ogni sottospazio vettoriale è in particolare uno spazio vettoriale.
Esercizio Provare che ogni sottospazio è in particolare un
sottogruppo .
I sottospazi vettoriali di R 2 sono dati da 0, dalle rette per l'origine e da R 2 stesso.
Esercizio L'intersezione di due sottospazio vettoriali è ancora un sottospazio vettoriale.
Combinazioni lineari
Se v1,...,vk sono vettori di uno spazio
vettoriale V e l1,...,l
k Î R allora
Si=1 k
li vi
si dice una combinazione lineare dei vettori
v1,...,vk . In particolare l v è una combinazione lineare di v, l1v1+ l2v2 è una combinazione lineare di v1, v2.
Proposizione L'insieme delle combinazioni lineari di v1,...,vk è un sottospazio di V che viene indicato con <v1,...,vk >.
La dimostrazione della proposizione precedente segue dalla definizione e viene lasciata come esercizio.
Definizione Poniamo in Rn e1:=(1,0,...,0) e2:=(0,1,...,0) en:=(0,0,...,1) Allora per ogni x=(x1,...,xn) ÎRn si ha x=x1e1+x2e2+ ...+xnen quindi ogni vettore di Rn si può scrivere come combinazione lineare di e1,...,en.
e1,...,en si dice, per motivi che vedremo più avanti, la base standard di Rn.
Osservazione Se A è una matrice di tipo nxm ed ei è un vettore colonna (matrice mx1) allora Aei è la i-esima colonna di A. Analogamente ei t è la i-esima riga di A. Funzioni lineari
Definizione Siano V, W due spazi vettoriali.Una funzione f: V ® W si dice lineare se per ogni v,zÎ V e per ogni per ogni l Î R si ha - f(v+z)=f(v)+f(z)
- f(l v)=l f(v)
In particolare una funzione lineare è un omomorfismo di gruppi. Le due condizioni precedenti possono essere riassunte nella condizione equivalente:
per ogni v,zÎ V e per ogni per ogni l, m Î R - f( lv+m z)= lf(v)+ m f(z)
Lemma Se f è una funzione lineare allora f(0)=0.
Dimostrazione f(0)=f(0+0)=f(0)+f(0). Sommando ad ambo i membri -f(0) si ha la tesi.
Questa stessa dimostrazione mostra che ogni omomorfismo tra gruppi porta l'elemento neutro nell'elemento neutro. Ad esempio log(1)=0.
Osserviamo che se f è una funzione lineare allora f(-v)=-f(v).
Una funzione lineare da V a W conserva le combinazioni lineari.
Questo significa che se v1,...,vk sono vettori di V e l1,...,l k Î R allora f(Si=1 k li vi)= Si=1 k lif( vi) Una dimostrazione formale di questo fatto segue dalla definizione di linearità per induzione su k.
Esempio di una funzione lineare che descrive una previsione elettorale.
Le rotazioni attorno all'origine in R2 come funzioni lineari
Consideriamo in R2 la rotazione di un angolo q in senso antiorario attorno all'origine. Chiamiamo rq: R2® R2 questa rotazione. Un punto di coordinate (r cos(a), r sen(a) ) viene portato da rq nel punto (r cos(a+q), r sen(a+q) ). Per le formule di addizione
| cos(a+q)=cos(a)cos(q)-sen(a)sen(q) |
|
| sen(a+q)=cos(a)sen(q)+sen(a)cos(q) |
|
La notazione matriciale ci pemette di separare il contributo di a (che varia da punto a punto) da quello di q (che è lo stesso per tutti i punti e dipende solo dalla rotazione). Precisamente abbiamo
| | æ
ç
ç
ç
è | | | ö
÷
÷
÷
ø | = | é
ê
ê
ê
ë | | | ù
ú
ú
ú
û | | æ
ç
ç
ç
è | | | ö
÷
÷
÷
ø | |
|
ed applicando questa formula alle coordinate dei punti
| | æ
ç
ç
ç
è | | | ö
÷
÷
÷
ø | = | é
ê
ê
ê
ë | | | ù
ú
ú
ú
û | | æ
ç
ç
ç
è | | | ö
÷
÷
÷
ø | |
|
Quindi le coordinate di
sono date da
| | é
ê
ê
ê
ë | | | ù
ú
ú
ú
û | | æ
ç
ç
ç
è | | | ö
÷
÷
÷
ø | |
|
Adesso la matrice 2x2
descrive la rotazione e la scrittura matriciale della rotazione di un vettore v di R2 visto come vettore colonna è rq (v)=Aq v dove tra Aq e v viene eseguita la moltiplicazione tra matrici. Da questa descrizione è evidente (proprietà distributive del prodotto tra matrici) che rq è lineare.
Esercizio Provare la forma matriciale delle formule di addizione, cioè
Aq Ab = Aq+b I precedenti esempi possono essere generalizzati associando ad una qualunque matrice una funzione lineare. Vedremo che questo è il modo in cui si costruiscono tutte le funzioni lineari.
Proposizione Se f: V ® W è una funzione lineare, v1,...,vk Î V , l1,...,l k Î R allora
f( Si=1 k li vi)= Si=1 k li f( vi)
Funzioni lineari associate a matrici
Teorema Se due funzioni lineari da Rm a Rm coincidono sulla base standard di Rm allora coincidono dappertutto.
Dimostrazione Siano f,g:Rm ® Rn tali che per ipotesi f(ei)=g(ei) per i=1,...,n. Allora se x=x1e1+x2e2+ ...+xnenÎRn si ha f(x)=f(x1e1+x2e2+ ...+xnen)= x1f(e1)+x2f(e2)+ ...+xnf(en)= x1g(e1)+x2g(e2)+ ...+xng(en)= g(x1e1+x2e2+ ...+xnen)=g(x) come volevamo dimostrare.
Sia A una matrice nxm. Associamo ad A la funzione fA :Rm ® Rn definita da fA(x) := Ax dove x viene considerato come vettore colonna a m componenti. Le proprietà distributive del prodotto tra matrici implicano che fA è lineare.
Infatti per ogni x, z Î Rm fA(x+z) = A(x+z) = Ax+Az = fA(x)+ fA(z) mentre per ogni x Î Rm , l R fA( lx)=A( lx)= l Ax= l fA(x) Teorema Sia g :Rm ® Rn una funzione lineare. Allora esiste una unica matrice A di tipo nxm tale che g=fA
Dimostrazione Definiamo A come la matrice che per i-esima colonna ha g(ei). Allora per costruzione g(ei)=Aei= fA(ei) Quindi g e fA coincidono sulla base standard e per il teorema
precedente abbiamo la tesi. Per ottenere l'unicità basta osservare che calcolando fA e fB sulla base standard otteniamo che A e B hanno tutte le colonne uguali e quindi coincidono.
Esempio Se v è un vettore riga (matrice mx1) allora fv(x)=v.x . Il teorema precedente quindi dice che per ogni funzione lineare f:Rm ® R esiste vÎ Rm tale che f(x)= v.x. Questo teorema vale anche nel caso di spazi di dimensione infinita (con una ipotesi di limitatezza) ed in questo contesto si chiama teorema di rappresentazione di Riesz. In particolare dal teorema segue che ogni funzione lineare
g:Rm ® R ha la forma g(x1,x2,..., xn)=a1x1+ ...+anxn per certi aiÎ R.
Proposizione Sia A una matrice mxn, B una matrice nxp. Allora fA·fB =fAB Dimostrazione Per ogni x ÎRp vale
fA·fB(x)= fA(Bx)=A(Bx)=(AB)x=fAB(x).
La proposizione precedente applicata al caso in cui A=B è una matrice quadrata fornisce
(fA)2=f(A2)
e più in generale (fA)k=f(Ak) per ogni k ÎN. La formula precedente vale per ogni k ÎZ se A è invertibile.
Corollario Sia A una matrice quadrata. A è invertibile se e solo se fA è invertibile. In questo caso (fA)-1=f(A-1).
Dimostrazione Sia A invertibile. Allora f(A-1)· fA=f(A-1)A=fI=1
Viceversa se fA è invertibile esiste un'inversa che per il teorema ha la forma fB. Segue che fAB =fI e per l'unicità del teorema AB=I da cui B è l'inversa di A.
Un modello dove troviamo la potenza di una matrice
Teoria della dipendenza lineare, basi
Definizione Uno spazio vettoriale V si dice generato da v1, ..., vk se ogni vettore di V può essere espresso come combinazione lineare di v1, ..., vk.
In modo equivalente V è generato da v1, ..., vk se <v1,...,vk > =V.
Per questo motivo il sottospazio vettoriale <v1,...,vk > viene chiamato il sottospazio generato da v1, ..., vk che vengono detti generatori.
Esempio I vettori e1, ..., en generano Rn.
Esercizio Se un sottoinsieme di v1, ..., vk genera V allora v1, ..., vk genera V.
Definizione v1, ..., vk Î V si dicono (linearmente) dipendenti se esiste (a1,a2,..., an)¹0 tale che a1v1+ ...+anvn=0
Si noti l'importanza del requisito (a1,a2,..., an)¹0 , senza questa richiesta tutti i vettori sarebbero dipendenti e la definizione perderebbe di significato!
Proposizione Le seguenti condizioni sono equivalenti - v1, ..., vk sono dipendenti
- È possibile esprimere un vettore tra v1, ..., vk come combinazione lineare degli altri
Dimostrazione 1 Þ 2 Se a1v1+ ...+anvn=0 con ai¹0 allora vi= -(a1/ai)v1 -... -(ai-1/ai)vi- -(ai+1/ai)vi+1-... -(ak/ai)vk
2 Þ 1 Se vi = c1v1+... ci-1vi-1+ ci+1vi+1+... ckvk allora c1v1+... ci-1vi-1- vi + ci+1vi+1+... ckvk=0
Vettori che non sono dipendenti si dicono indipendenti.
Proposizione Le seguenti condizioni sono equivalenti - v1, ..., vk sono indipendenti
- Se a1v1+ ...+anvn=0 allora (a1,a2,..., an)=0
Dimostrazione Immediata dalla definizione.
Esercizio Se v1, ..., vk sono indipendenti allora ogni sottoinsieme di {v1, ..., vk} è formato da vettori indipendenti.
Esercizio Provare che vettori indipendenti sono sempre non nulli.
Definizione Siano a1,..., anÎ R. Il sottoinsieme H di Rn costituito da tutti gli (x1,...,xn) tali che a1x1+ ...+anxn=0 si dice un iperpiano di Rn.
Gli iperpiani di R2 sono le rette per l'origine. Gli iperpiani di R3 sono i piani per l'origine.
Ogni iperpiano è un sottospazio vettoriale. Per l'esempio del paragrafo precedente ogni iperpiano può essere visto come il luogo dei punti x tali che una funzione lineare h da Rn a R si annulla, cioè H={x|h(x)=0}.
Proposizione Sia W un sottospazio di Rn che contiene k vettori indipendenti e sia H un iperpiano. Allora WÇ H contiene k-1 vettori indipendenti.
Dimostrazione Siano w1,...,wk vettori di W indipendenti. Sia H={x|h(x)=0} l'iperpiano considerato. Se h(wi)=0 per almeno k-1 valori dell'indice i allora wi appartengono a WÇ H per questi valori e la tesi è dimostrata. Possiamo quindi supporre h(wk)¹0. Poniamo mi:=h(wk)wi -h(wi)wk per i=1,...,k-1. È immediato verificare che h(mi)=0, quindi mi Î H. Siccome W è un sottospazio abbiamo anche mi Î W quindi mi Î WÇ H . Affermo che mi sono indipendenti. Consideriamo una combinazione lineare Si=1 k ai mi=0 Vale
0=Si=1 k ai mi= Si=1 k ai h(wk)wi - [Si=1 k ai h(wi)]wk
e quindi per l'indipendenza dei wi segue ai h(wk)=0 per i=1,...,k-1.
Siccome h(wk)¹0 segue ai =0 per i=1,...,k-1 come volevamo dimostrare.
Se A è una matrice nxm allora l'equazione matriciale Ax=0 dove x=(x1,...,xm)t Î Rm si dice un sistema lineare nelle m incognite x1,...,xm . Il sistema lineare è formato da n equazioni. Se aij è l'elemento di posto (i,j) di A allora la i-esima equazione è data da ai1 x1+ ai2 x2 + ...+aim xm=0 A si dice la matrice associata al sistema Ax=0. Ad esempio il sistema lineare
ha per matrice associata la matrice 2x2
Teorema Sia A una matrice nxm con n<m. Allora il sistema lineare Ax=0 ammette almeno una soluzione non nulla x Î Rm
Dimostrazione Definiamo Hi come l'iperpiano luogo dei punti x tali che ai1 x1+ ai2 x2 + ...+aim xm=0 Allora le soluzioni del sistema corrispondono a H1 ÇH2 Ç ...ÇHn
Rm contiene m vettori indipendenti (ad esempio la base standard). Quindi per la proposizione H1 contiene m-1 vettori indipendenti.
Sempre per la proposizione H1ÇH2 contiene m-2 vettori indipendenti.
Continuando in questo modo H1 ÇH2 Ç ...ÇHn contiene m-n vettori indipendenti.
Per ipotesi m-n>0, quindi esiste almeno un vettore indipendente (in particolare non nullo) che è soluzione.
Teorema Sia V uno spazio vettoriale. Siano { v1, ..., vk} vettori indipendenti di V.
Siano { w1, ..., ws} vettori generatori di V.
Allora k £s.
Dimostrazione Per ipotesi per i=1,...,k si può si scrivere vi=Sj=1 s aij wj per certi coefficienti aij . Consideriamo la combinazione lineare Si=1 k ci vi= Si=1 k ci Sj=1 s aij wj= Sj=1 s wj[Si=1 k ci aij ] Se per assurdo k>s allora il sistema lineare omogeneo Si=1 k ci aij =0 per j=1,...,s nelle incognite ci ha una soluzione non nulla c'i per il teorema precedente e quindi per tale soluzione sostituendo nella combinazione lineare precedente si ottiene Si=1 k c'i vi=0 contraddicendo l'ipotesi per cui { v1, ..., vk}
sono vettori indipendenti di V. Quindi k £s come volevamo.
Definizione Sia V uno spazio vettoriale. L'insieme { v1, ..., vk} di vettori di V si
dice una base di V se - { v1, ..., vk} sono generatori
-
{ v1, ..., vk} sono indipendenti
Teorema fondamentale della teoria della dimensione Due basi di uno spazio vettoriale hanno lo stesso
numero di elementi.
Dimostrazione Siano { v1, ..., vk} , { w1, ...,
ws} due basi di V. In particolare - { v1, ..., vk} sono indipendenti
- { w1, ..., ws} sono generatori
e dal teorema k £s.
Analogamente abbiamo anche che - { v1, ..., vk} sono generatori
- { w1,
..., ws} sono indipendenti
e dal teorema s £k. Quindi s=k come
volevamo.
Definizione La dimensione di uno spazio vettoriale V è il numero di elementi di
una sua base, e viene indicata con dim V
Esempio dim Rn
=n infatti la base standard { e1, ..., ee} è una base costituita da n
elementi.
Esercizi - Provare che se { v1, ..., vk} sono vettori
indipendenti in uno spazio vettoriale V di dimensione n, allora k £n.
- Provare
che la dimensione di V coincide con il massimo numero di vettori indipendenti che si possono trovare in V.
-
Provare che se { v1, ..., vk} sono vettori generatori di uno spazio vettoriale V di dimensione
n, allora k ³n.
- Provare che la dimensione di V coincide con il minimo numero di
vettori generatori che si possono trovare in V.
- Provare che se v1, ..., vk sono vettori
linearmente dipendenti in V e f: V® W è una funzione lineare allora f(v1),
..., f(vk) sono linearmente dipendenti . Dedurre che se f(v1), ..., f(vk) sono
indipendenti allora v1, ..., vk sono indipendenti.
- Provare, usando l'esercizio precedente,
che se f: V® W è una funzione lineare e V' è un sottospazio di V allora f(V')
è un sottospazio di W e vale dim V'³ dim f(V')
Proposizione (coordinate rispetto a una base)
Sia v1, ..., vn una base di V. Allora per ogni v in V
esistono unici x1, ..., nn tali che
v=x1v1+...+ xnvn.
L'esistenza segue dal fatto che v1, ..., vn sono
generatori. L'unicità segue dal fatto che sono indipendenti.
Completamento di vettori indipendenti ad una base Dati { v1, ..., vk} vettori
indipendenti in uno spazio vettoriale V di dimensione n, è sempre possibile trovare
{ vk+1, ..., vn} tali che { v1, ..., vn} formano una base.
Infatti se { v1, ..., vk} non è già una base segue che < v1, ...,
vk > è contenuto propriamente in V, scegliendo vk+1 non contenuto in < v1,
..., vk > si ottiene che { v1, ..., vk, vk+1} sono ancora indipendenti.
Infatti data la combinazione lineare Si=1 k+1 ci
vi=0 otteniamo ck+1=0, altrimenti vk+1 sarebbe combinazione lineare dei
precedenti. Quindi rimane Si=1 k ci vi=0 e
siccome { v1, ..., vk} sono indipendenti segue la tesi. Continuando in questo modo aggiungiamo
eventualmente vk+2, vk+3, ...., fino a che non troviamo una base.
Estrazione di una base da vettori generatori Dati { v1, ..., vk} vettori generatori in uno spazio vettoriale V di dimensione n, è sempre possibile trovare un sottoinsieme di n elementi tra i precedenti che formano una base. Infatti se { v1, ..., vk} non è già una base, per la
proposizione esiste un vettore dell'insieme { v1, ..., vk} che è combinazione lineare dei rimanenti. Allora i rimanenti sono ancora generatori. Infatti se per semplicità vk è combinazione lineare di v1,.., vk-1, cioè se vk=Si=1 k-1 ci vi per certi ci , ogni vettore v di V che si può scrivere come combinazione dei generatori v=Si=1 k ai vi si può anche scrivere come v=Si=1 k-1 ai vi+ ak vk = Si=1 k-1 ai vi+ ak Si=1 k-1 ci vi= =Si=1 k-1 (ai +ak ci) vi e quindi è combinazione lineare di v1,.., vk-1 che sono ancora generatori.
Se A è un sottospazio di uno spazio vettoriale B, allora dim A£ dim B
Se A è un sottospazio di B tale che dim A = dim B, allora A=B.
Teorema Sia V uno spazio vettoriale di dimensione n. Se v1,.., vn sono vettori indipendenti di V allora formano una base.
Dimostrazione Si può completare {v1,.., vn} ad una base costituita da n elementi che quindi coincide con {v1,.., vn} .
Teorema Sia V uno spazio vettoriale di dimensione n. Se v1,.., vn sono vettori generatori di V allora formano una base.
Dimostrazione Si può estrarre da {v1,.., vn} una base costituita da n elementi che quindi coincide con {v1,.., vn} .
Esercizio Provare che se f: V ® W è una funzione lineare e V' è un sottospazio di V, allora f(V') è un sottospazio di W e vale dim f(V')£ dim V'
Matrice associata ad una funzione lineare
Sia f: V ® W una funzione lineare.
Fissiamo u ={v1...vn}
base di V e w ={w1...wm} base di W. Allora è definita una matrice
M(f) w,u mxn la cui j-esima colonna è data dalle coordinate di f(vj) rispetto a
{w1...wm}. In formula il coefficiente aij di M(f)
è dato da
f(vj)= Si=1maij.
Se indichiamo con x le coordinate di v rispetto a u, allora
le coordinate di f(v) rispetto a w sono date da M(f) w,u x,
come si verifica subito applicando f ai vettori della base vj} che hanno coordinate date da
ej, infatti M(f) w,u ej è la j-esima colonna
di M(f) w,u.Siano x le coordinate di v rispetto a w,u
si chiama matrice di cambiamento di coordinate.
Proposizione Con ovvie notazioni
M(g) y,w M(f) w,u =
M(gf) y,u
Dimostrazione
Siano x le coordinate di v rispetto a u, allora
le coordinate di f(v) rispetto a w sono date da M(f) w,u x
e quindi le coordinate di gf(v) rispetto a y sono date da
M(g) y,w M(f) w,u x
come volevamo.
Corollario Sia
f: V Î V una funzione lineare e siano
u, w due basi di V.
- M(1) w,u =M(1) u,w-1
- Posto C=M(1) w,u
allora M(f) u,u=C-1M(f) w,w
C
Il punto 2 del corollario precedente afferma che le matrice di una funzione lineare da V in se
rispetto a basi diverse sono simili.
Nucleo e immagine
Consideriamo una funzione lineare f: V ®
W .
Definizione Il nucleo di f è l'insieme {v Î V|f(v)=0}
che viene indicato con Ker(f).
L'immagine di f viene indicata con Im(f).
Teorema Ker(f)
è un sottospazio di V. Im(f) è un sottospazio di W.
EsercizioSia
f: V ®
V una funzione lineare. Provare che
-
Ker f2Ê Ker f
- Im f2 Í Im f
Teorema della dimensione Sia f: V ® W una funzione lineare. Allora dim Ker(f)+dim Im(f)=dim V Dimostrazione Poniamo k=dim Ker(f), n=dim V. Sia {v1,.., vk} una base di Ker(f), e completiamola con {vk+1,.., vn} ad una base di V. La tesi è
dim Im(f)=n-k.
Quindi è sufficiente dimostrare che gli n-k vettori {f(vk+1),.., f(vn)}
formano una base di Im(f). - {f(vk+1),.., f(vn)} generano Im(f).
Infatti se w appartiene a Im(f) esiste v in V tale che w=f(v). Siccome {v1,.., vn} è
una base di V esistono coefficienti reali ci tali che v=Si=1
n ci vi. Pertanto w=f(v)=f(Si=1 n
ai vi)= Si=1 n ai f(vi)=
Si=k+1 n ai f(vi)
come volevamo perchè
f(vi)=0 per i=1,...,k. - {f(vk+1),.., f(vn)} sono indipendenti.
ConsideriamoSi=k+1 n ai f(vi)=0
Allora per linearità f(Si=k+1 n ai vi)=0
e quindi Si=k+1 n ai vi appartiene a Ker(f)
e si può scrivere come combinazione lineare di {v1,.., vk} . Pertanto esistono
coefficienti reali ci tali che Si=k+1 n
ai vi =Si=1 k ci vi
Portando a primo membro Si=1 k (-ci)
vi+ Si=k+1 n ai vi =0 da
cui ai =0 per i=k+1,...,n come volevamo.
Notazione Poniamo
Ker A:=Ker fA, Im A:=Im fA Ker A corrisponde allo spazio delle soluzioni del sistema
lineare omogeneo Ax=0.
Im A è lo spazio generato dalle colonne di A. Infatti se A è una matrice nxm
con colonne A1,...,Am allora un elemento di Im A si scrive come fA(x)= x1
A1+...+xmAm per qualche x=(x1,...,xm) ed è quindi
combinazione lineare delle colonne di A.
Definizione Il rango di A (rango per colonne) è per definizione la
dimensione di Im A, cioè è la dimensione dello spazio generato dalle colonne di A. Il rango si
indica con la dicitura rk (dall'inglese rank). In formula rk(A):=dim Im A
Esercizio Siano V, W spazi vettoriali dela stessa dimensione. Provare che f:V ® W
è iniettiva se e solo se è suriettiva.
Teorema Sia A una matrice nxn. A è
invertibile se e solo se rk(A)=n.
Dimostrazione A è invertibile se e solo se fA
è invertibile per il corollario. Dal teorema della dimensione segue che fA
è invertibile se e solo se f
A è suriettiva ( si veda l'esercizio precedente) e quindi se e solo se rk(A)=dim Im fA=n.
Corollario Una matrice è invertibile se esiste B tale che AB=I.
In questo caso vale anche BA=I.
Dimostrazione Se AB=I allora fA è suriettiva perchè
per ogni x vale fA (fB(x))=fAB(x)=fI(x)=x.
Quindi per il teorema precedente fA è invertibile.
Inoltre B è iniettiva e per il teorema della dimensione è anche suriettiva e quindi invertibile.
Sia C l'inversa di B. Allora C=IC=(AB)C=A(BC)=A e quindi BA=BC=I come volevamo.
Applicazioni ai sistemi lineari
Il sistema lineare omogeneo Ax=0 ha per soluzioni esattamente il sottospazio Ker A.
Quindi l'insieme delle soluzioni di un sistema lineare omogeneo è sempre
un sottospazio vettoriale che per il teorema della dimensione ha
dimensione pari a numero delle incognite -rg(A).
Teorema di struttura
Sia x' una soluzione del sistema Ax=b. Allora tutte le soluzioni di Ax=b
hanno la forma z+x' con z in Ker A, si può scrivere che lo spazio delle soluzioni
è pari a Ker A+x'.
Dimostrazione A(z+x')=Az+Ax'=0+b=b. Viceversa se Ay=b
allora A(y-x')=Ay-Ax'=b-b=0 e quindi y-x' appartiene a Ker A. Segue che y appartiene
a Ker A+x' come volevamo.
Esercizio Provare che le seguenti condizioni sono equivalenti per una matrice quadrata nxn A
- rg(A)=n
- Ax=0 ha solo la soluzione nulla
- per ogni b Ax=b ammette una unica soluzione.
Teorema di Rouchè-Capelli
Il sistema lineare Ax=b ammette soluzione se solo se rg(A)=rg(A|b).
Dimostrazione Siano A1... A
n le colonne di A. Il sistema lineare Ax=b ammette soluzione se e solo se
esiste x tale che A1x1+... +Anxn=b
se e solo se b è combinazione lineare delle colonne di A
se e solo se gli spazi delle colonne di A e di (A|b) sono uguali.
5. Basi ortonormali e spazi ortogonali
Lemma Se {v1,.., vk} sono vettori di Rn tali che vi. vj= d ij allora sono linearmente indipendenti.
Dimostrazione Considero Si=1 k ci vi=0 Moltiplicando scalarmente ambo i membri per vj rimane cj=0 come volevamo.
Definizione Una base ortonormale di un sottospazio W di Rn è una base {v1,.., vk} di W tale che vi. vj= d ij
Per il lemma, se dimW=k è sufficiente trovare {v1,.., vk} vettori di W tali che vi. vj= d
ij ed otteniamo una base ortonormale.
Proposizione
Siano {v1,.., vn} le colonne di una matrice quadrata
nxn A. Allora le seguenti proprietà sono equivalenti:
- {v1,.., vn} è
una base ortonormale di Rn
- A è una matrice ortogonale.
La proprietà più importante delle basi ortonormali è data dal seguente
Teorema dei coefficienti di Fourier Sia {v1,.., vk} una base ortonormale di un sottospazio W di Rn . Allora se w è un vettore di W vale w=Si=1 k (w. vi) vi ed i coefficienti (w. vi) della combinazione lineare con cui si esprime w come combinazione lineare della base ortonormale si dicono coefficienti di Fourier.
Dimostrazione Sia w=Si=1 k ci vi con ci da determinare.
Moltiplicando ambo i membri scalarmente per vj otteniamo w. vj= cj come volevamo.
Teorema di Pitagora generalizzato Sia {v1,.., vk} una base ortonormale di un sottospazio W di Rn . Allora se w è un vettore di W vale |w|2=Si=1 k (w. vi) 2
Data una base qualunque di un sottospazio di Rn , si può sempre trovare una base ortonormale mediante l'algoritmo di Gram-Schmidt.
Perchè l'algoritmo di Gram-Schmidt funziona.
Per l'algoritmo di Gram-Schmidt è sempre possibile completare una base ortonormale di un sottospazio di Rn ad una base ortonormale di Rn stesso.
Definizione Sia W un sottospazio di Rn . Poniamo W^:= {v Î Rn | v. w=0 "w Î W} W^ si dice lo spazio ortogonale a W.
Criterio di appartenenza all'ortogonale Sia {w1,.., wk} una base di W. Allora v Î W^ se solo se v. wi=0 per i=1,...,k
Teorema (dimensione dell'ortogonale) W^ è un sottospazio di Rn e vale dim W^ = n-dim W Dimostrazione - Pongo dim W=k e considero una base ortonormale {w1,.., wk} di W
- Completo {w1,.., wk} ad una base {w1,.., wk,wk+1,.., wn} di Rn .
- Applico l'algoritmo di Gram-Schmidt alla base precedente ed ottengo {w1,.., wk,vk+1,.., vn} base ortonormale di Rn (i primi k vettori sono rimasti invariati perchè erano una base ortonormale di W, infatti l'algoritmo di Gram-Schmidt permette di completare una base ortonormale di un sottospazio ad una base ortonormale di Rn ).
- Verifico che W^ è generato da {vk+1,.., vn}. Segue dalla costruzione che vi Î W^ per i=k+1,...,n. Viceversa se w Î W^ possiamo scrivere w come combinazione lineare w=Si=1 kciwi+ Sj=k+1 ncjvj Moltiplicando scalarmente ambo i membri dell'uguaglianza precedente per ws per s=1,...,k otteniamo 0=cs per s=1,...,k e quindi w=Sj=k+1 ncjvj risulta combinazione lineare di {vk+1,.., vn}. Questi ultimi n-k vettori sono indipendenti e quindi dim W=n-k come volevamo.
Proposizione (W^ )^ =W
Dimostrazione Se x Î W e y Î W^ allora x. y=0, quindi x Î (W^ )^ , cioè WÍ (W^ )^ Per il teorema precedente dim (W^ )^ =n- dim W^ =dim W e quindi l'inclusione precedente è un'uguaglianza come volevamo.
Esercizio Provare che se AÍ B allora B^ Í A^ . Vale il viceversa?
Teorema fondamentale dell'algebra lineare Sia A una matrice nxm - (Ker A)^ =Im(tA)
- rk(A)=rk(tA)
Il secondo punto del teorema fondamentale si esprime dicendo che la dimensione dello spazio delle colonne di A (rango per colonne) è uguale alla dimensione dello spazio delle righe di A (rango per righe).
Dimostrazione del teorema fondamentale dell'algebra lineare Prendo x Î Ker A e y Î Im(tA). Quindi esiste z Î Rn tale che y=tAz.
Allora x. y= tyx=t(tAz)x= (tzA)x=tz(Ax)=tz0=0
Quindi y Î Ker A ^ ed abbiamo provato l'inclusione (Ker A)^ ÊIm(tA). Da questa inclusione segue la disuguaglianza rk(tA)=dim Im(tA) £dim (Ker A)^=n-dim Ker A =dim Im(A)=rk(A) La disuguaglianza precedente vale per tutte le matrici A, quindi sostituendo tA al posto di A otteniamo rk(A)=rk[t(tA)]£rk(tA) e questo dimostra il secondo punto. Ma anche il primo punto segue di conseguenza perchè (Ker A)^ e Im(tA) sono due spazi uno contenuto nell'altro che hanno la stessa dimensione pari a rk(A) e quindi coincidono.
Commenti sul teorema fondamentale dell'algebra lineare.
Esercizio Provare che se A è una sottomatrice di B allora rk(A)£rk(B).
Esercizio Provare che se A è una matrice nxm allora 0£rk(A)
£min(n,m).
Proposizione (rango=numero dei pivot)
Sia A una matrice e sia S una sua riduzione a scalini mediante operazioni elementari
di tipo I e III. Allora il rango di A è pari al numero dei pivot di S.
Dimostrazione Lo spazio delle righe rimane invariato per operazioni elementari,
che sono tutte operazioni invertibili. Basta allora osservare che
le righe (non nulle) di una matrice a scalini sono indipendenti,
che è evidente dalla definizione.
L'algoritmo di Gauss, per la proposizione precedente, permette di calcolare
il rango di una matrice.
Prodotto cartesiano di due spazi vettoriali
Il modo in cui si costruisce R2 a partire da due copie di R (prima e seconda componente) ha la seguente utile generalizzazione.
Se V, W sono due spazi vettoriali, sul prodotto cartesiano VxW è definita una struttura naturale di spazio vettoriale con le operazioni - (v,w)+(v',w'):=(v+v',w+w') per ogni v,v' Î V, per ogni w,w' Î W.
- c(v,w):=(cv,cw) per ogni v Î V, w Î W, c Î R.
Notiamo che in particolare (v,w)=(v,0)+(0,w) Da questa osservazione segue facilmente il
Teorema dim VxW=(dim V)+(dim W)
Dimostrazione Se {v1,.., vk} è una base di V e {w1,.., wm} è una base di W allora i k+m elementi (vi,0), (0,wj) Î VxW per i=1,...,k, j=1,...,m formano una base di VxW.
Esempio Rn xRm =Rn+m Somma di due sottospazi
Se A, B sono due sottospazi di uno spazio vettoriale V, poniamo A+B:={a+b|a Î A, b Î B }
Proposizione A+B è un sottospazio di V che si dice sottospazio somma di A e B.
Esempio 1 Per ogni sottospazio W di Rn abbiamo W + W^ = Rn
Esempio 2 Per ogni sottospazio W di Rn abbiamo W+W=W
I due esempi precedenti mostrano che la dimensione della somma di due sottospazi non dipende soltanto dalla dimensione di ciascuno. Precisamente vale il
Teorema (formula di Grassmann) Se A, B sono due sottospazi di uno spazio vettoriale V, vale dim(A+B)+dim (A Ç B)= dimA+dim B Dimostrazione Definisco le seguenti due funzioni lineari
f:AxB ® A+B g:A Ç B ® AxB dalle formule f(a,b):=a+b, g(a):=(a,-a). Affermo che - g è iniettiva, infatti Ker(g)=0
- f è suriettiva (evidente)
- Im(g)=Ker(f).
Dimostriamo che Im(g) è contenuto in Ker(f). Se (a,-a) è un elemento di Im(g) allora f(a,-a)=a-a=0 e quindi (a,-a) appartiene a Ker(f). Viceversa sia (a,b) un elemento di Ker(f). Quindi a+b=0, da cui a=-b e quindi a appartiene anche a B, pertanto appartiene a A Ç B. Quindi (a,b)=(a,-a) è l'immagine di a tramite g ed appartiene a Im(g).
Possiamo concludere applicando il teorema della dimensione. Infatti dim A+dim B=dim AxB=dim Im(f)+dim Ker (f)= dim (A+B)+ dim Im(g)= dim(A+B)+dim(A Ç B)-dim Ker(g)= dim(A+B)+dim(A Ç B) come volevamo.
Denotiamo con Sn il gruppo delle permutazioni sull'insieme di n elementi {1,2,¼n}. Sn contiene n! elementi. Per ogni p Î Sn denotiamo con e(p) il segno di p.
Sia A una matrice quadrata n×n e sia aij il suo elemento di posto (i,j).
Definizione Il determinante di A é dato dalla formula
| det(A)= |
å
p Î Sn
| e(p)a1p(1)a2p(2)¼anp(n) |
|
Il determinante è una funzione det:Mn ® R. Il determinante è definito sugli n2 coefficienti di A. Identificando Mn con Rn2 il determinante può essere visto come una funzione di n2 variabili det: Rn2® R. Il determinante non è una funzione lineare, ad esempio in generale det(A+B) è diverso da det(A)+det(B). Esempio Se A é una matrice 1×1, contiene un unico elemento a. La sommatoria nella definizione di di determinante contiene un unico elemento (l'identitá) che ha segno 1. Quindi
Questo è l'unico caso in cui il determinante è una funzione lineare. Esempio Se A é una matrice 2×2, la sommatoria nella definizione di di determinante contiene due elementi: l'identitá che ha segno 1 per cui p(1)=1, p(2)=2 e la trasposizione che ha segno -1 per cui p(1)=2, p(2)=1. Quindi
Proposizione Il determinante soddisfa le seguenti proprietá:
- D1 det é lineare su ciascuna riga. Questa proprietà supplisce la mancanza di linearità del determinante. Infatti gli elementi della riga i-esima compaiono nell'espressione una volta in ciascun addendo sempre con grado 1.
- D2 Sia A¢ ottenuta da A scambiando due righe (operazione elementare di tipo I). Allora det (A)=-det(A¢).
- D3 det(I)=1
Lemma det(cA)=cndet(A) per ogni scalare c. In particolare det(-A)=(-1)ndet(A).
Dimostrazione Calcolando det(cA) dalla formula che definisce il determinante, ogni addendo ha la forma
e(p)(ca)1p(1)(ca)2p(2)¼(ca)np(n)= cne(p)a1p(1)a2p(2)¼anp(n)
Teorema. Caratterizzazione del determinante Sia f: Mn®R una funzione che soddisfa le seguenti proprietá
- D1f é lineare su ciascuna riga.
- D2 Sia A¢ ottenuta da A scambiando due righe (operazione elementare di tipo I). Allora f (A¢)=-f (A).
- D3 f(I)=1
Allora f=det. Quindi il determinante è l'unica funzione che soddisfa D1, D2, D3.
La dimostrazione sará svolta nei seguenti passi.
Lemma Sia f: Mn®R una funzione che soddisfa D1, D2, D3. Allora vale
- D4 Se A é una matrice con due righe uguali allora f(A)=0. Dimostrazione
- D5 Se A é una matrice con una riga nulla allora f(A)=0 Dimostrazione
- D6 Se A¢ é ottenuta da A sostituendo alla riga Aj la riga Aj+cAi per i ¹ j (operazione elementare di tipo III) allora f(A')=f(A) Dimostrazione
- D7 Se D é una matrice diagonale con d1...dn elementi diagonali allora f(D)=d1¼dn. Dimostrazione
Dimostrazione del teorema
Sia A una matrice. Possiamo effettuare su A operazioni elementari di tipo I (scambio di righe) e di tipo III (somma di un
multiplo di una riga ad un'altra) e ridurre A a forma a scalini T.
Se A' é ottenuta da A mediante un' operazione elementare di tipo I abbiamo f(A')=-f(A) (D3) e det(A')=-det(A). Se A' é ottenuta da A mediante un'operazione elementare di tipo III allora f(A')=f(A) e det(A')=det(A) (D1 e D4). Distinguiamo due casi.
- Se T ha l'ultima riga nulla allora da D1 f(T)=det(T)=0. Quindi dopo avere effettuato una successione di operazioni elementari di tipo I e III sia f e det coincidono su T, e quindi dovevano coincidere anche inizialmente su A, cioé f(A)=det(A)=0.
- Se T non ha l'ultima riga nulla allora è triangolare con tutti gli elementi sulla diagonale diversi da zero e mediante operazioni elementari di tipo I e III si riconduce T a forma diagonale D. Quindi dopo avere effettuato una successione di operazioni elementari di tipo I e III sia f e det coincidono su D per D7, e quindi dovevano coincidere anche inizialmente su A, cioé f(A)=det(A)=0.
In entrambi i casi si ha f(A)=det(A) come volevamo.
In particolare riassumiamo le proprietá che abbiamo visto
- D4 Se A é una matrice con due righe uguali allora det(A)=0
- D5 Se A é una matrice con una riga nulla allora det(A)=0
- D6 Se A¢ é ottenuta da A sostituendo alla riga Aj la riga Aj+cAi per i ¹ j (operazione elementare di tipo III) allora
det(A')=det(A) - D7 Se D é una matrice diagonale allora det(D)=d1¼dn.
Aggiungiamo
- D8 Se T é una matrice triangolare allora det(T)=d1¼dn.
Infatti se T ha l'ultima riga nulla il suo determinante vale zero. Altrimenti con operazioni elementari di tipo III T è equivalente ad una matrice diagonale con gli stessi elementi diagonali di T (annullo gli elementi sopra a ciascun elemento sulla diagonale, cominciando dall'ultima colonna). - D9 det(A)=det(tA)
Dimostrazione
Ricordiamo che
| det(A)= |
å
p Î Sn
| e(p) a1p(1)¼anp(n) |
|
Se chiamo p(i)=j allora aip(i)=ap-1(j)j ed al variare di i da 1 a n anche j copre tutti i naturali da 1 a n. Quindi l'addendo a1p(1)¼anp(n) é uguale a ap-1(1)1¼ap-1(n)n . Inoltre e(p) = e(p-1) perché gli scambi che danno p, composti in ordine inverso danno p-1. Posto bij=aji (coefficienti della matrice trasposta) abbiamo
| det(A)= |
å
p Î Sn
| e(p) a1p(1)¼anp(n) = |
å
p Î Sn
| e(p) b1p-1(1)¼bnp-1(n)= |
|
| = | -->
å
q Î Sn
| e(q) a1q(1)¼anq(n)= | det
| (tA) |
|
Queste proprietá portano ad un algoritmo pratico di calcolo del det: applica operazioni elementari di tipo I e III su A fino a che non si arriva a forma triangolare T e tieni conto che ogni tipo I (scambio) cambia il segno. Quindi det(A)=det(T) se il numero di scambi è pari e det(A)=-det(T) se il numero di scambi è dispari. Per calcolare det(T) si può usare D8.
- D10 Sviluppo per la i-esima riga
Chiamo Aij la sottomatrice ottenuta da A eliminando la riga i-esima e la colonna j-esima. Vale
| det(A)= | n
å
j=1
| aijdet Aij |
|
Per la dimostrazione, utilizzando D2, possiamo ricondurci al caso i=1 (sviluppo lungo la prima riga). In questo caso possiamo dividere la sommatoria della definizione di determinante nelle seguenti n sommatorie
| | det
| (A) = |
å
p Î Sn, p(1)=1
| e(p)a11a2p(2)¼anp(n)+ |
å
p Î Sn, p(1)=2
| e(p)a12a2p(2)¼anp(n)+ |
|
| ¼+ |
å
p Î Sn, p(1)=n
| e(p)a1na2p(2)¼anp(n)= |
|
| a11 |
å
p Î Sn, p(1)=1
| e(p)a2p(2)¼anp(n)+¼+a1n |
å
p Î Sn, p(1)=n
| e(p)a2p(2)¼anp(n) |
|
Nell'ultima formula la prima sommatoria corrisponde a detA11, la seconda a -detA12, l'ultima a (-1)ndetA1n.
Teorema rk(A)=n se e solo se det(A) ¹ 0
Dimostrazione rk(A)=n se e solo se mediante operazioni elementari di tipo I, III si arriva a una matrice a scalini con tutti i pivot non nulli, quindi ad una matrice triangolare con tutti gli elementi diagonali diversi da zero. Solo in questo caso det é diverso da zero.
Corollario A é invertibile se e solo se det(A) ¹ 0
Formula di Cauchy-Binet
det(AB)=det(A)det(B)
Dimostrazione
Se det(B)=0 allora fB non é iniettiva, quindi fAB = fA·fB
non é iniettiva da cui det(AB)=0. Se det(B) ¹ 0 allora considera
f(A):=det(AB)/det(B).
f soddisfa D1, D2, D3 e quindi
f(A)=det(A) dalla caratterizzazione del determinante come volevamo.
Relazione tra rango e determinante
Proposizione
Sia A una matrice mxn. Allora A ha rango maggiore o uguale a k se solo se esiste una
sottomatrice kxk di A con determinante non nullo.
Dimostrazione Se A contiene k righe indipendenti allora la sottomatrice corrispondente
kxn estratta ha spazio delle colonne di dimensione k e quindi si può estrarre
ulteriormente una sottomatrice kxk di rango k, che quindi ha determinante non nullo. Viceversa
se esiste una sottomatrice kxk di rango k allora la sottomatrice kxn corrispondente ha ancora
rango k (guardando le colonne) e quindi le sue righe sono indipendenti ed il rango di A è
maggiore o uguale a k.
Sistemi lineari omogenei nx(n+1)
Proposizione Sia A una matrice omogenea nx(n+1) di rango n.
Indichiamo con A(i) il determinante della sottomatrice ottenuta cancellando da A
la i-esima colonna.
Il sistema lineare Ax=0 ha una base per le soluzioni costituita da x=(x1,
...xn+1) con xi=(-1)iA(i)
Dimostrazione Impiliamo sopra ad A la sua prima colonna ed otteniamo
una matrice A' con due righe uguali che quindi ha determinante pari a zero. Sviluppando
il determinante rispetto alla prima riga si ottiene che la soluzione data è
soluzione della prima equazione. Considerando una nuova matrice A' dove la rige i-esima è
ripetuta due volte e ragionando allo stesso modo si ottiene che la soluzione data
è soluzione della i-esima equazione. Siccome lo spazio delle soluzioni ha dimensione 1
e per la proposizione precedente la soluzione data è non nulla segue la tesi.
Definizione
Sia V uno spazio vettoriale e T:V ® V
una applicazione lineare. Un vettore v Î V
non nullo si dice autovettore di T con autovalore
l se vale
T(v)= l v
Questo significa che v è portato da T in un multiplo di se stesso.
L'insieme degli autovalori di T si dice lo spettro di T.
Osserviamo subito che il requisito che l'autovettore v sia non nullo è essenziale, altrimenti tutti i numeri reali c sarebbero autovalori corrispondenti a v=0 perchè T(0)=c0 è una identità sempre soddisfatta.
Autovettori ed autovalori di una matrice quadrata A sono per definizione autovalori ed autovettori di fA.
Questo significa che v Î R
n è un autovettore di A con autovalore
l se vale
Av= l v
Per semplicità tratteremo soprattutto il caso degli autovalori ed autovettori di una matrice, analogamente si potrebbe considerare il caso generale.
Esempi Ogni vettore non nullo è autovettore della matrice identità con autovalore 1, infatti Iv=1v per ogni v.
Quindi lo spettro dell'identità è costituito da {1}.
Generalizzando, per ogni numero reale c,
ogni vettore non nullo è autovettore della matrice cI con autovalore c, infatti (cI)v=cv per ogni v.
Quindi lo spettro di cI è costituito da {c}. Se c=0 otteniamo lo spettro della matrice zero.
Se D è una matrice diagonale con elementi sulla diagonale
{c1, ..., cn} allora ei
è autovettore di D con autovalore ci.
Dimostreremo tra breve che non ci sono altri autovalori, cioè lo spettro di una matrice diagonale è costituito dagli elementi sulla diagonale. Le matrici diagonali si comportano quindi in modo molto semplice rispetto allo studio degli autovalori ed autovettori.
Definizione Il polinomio caratteristico di una matrice A è definito dall'espressione
pA(t):=det(A-tI)
dove I è la matrice identità .
L'introduzione del polinomio caratteristico è motivata dal seguente
Lemma Lo spettro di A è costituito dalle radici (reali)
del polinomio caratteristico di A.
Dimostrazione
Dobbiamo provare che l
è un autovalore di A se e solo se pA( l )=0.
Infatti l
è un autovalore di A se e solo se esiste v non nullo tale che
Av= l v se e solo se esiste v non nullo
tale che (A- l
I)v=0 se e solo se Ker(A- l
I) è diverso da zero
se e solo se (A- l
I) non è iniettiva se e solo se
det(A- l I)=0
Osservazione Se v è un autovettore di A
con autovalore l allora
è immediato verificare per ogni reale non nullo c
che cv è un autovettore di A
con lo stesso autovalore l. Se
v1, v2 sono autovettori di A
con lo stesso autovalore l
allora v1+v2 (se non è nullo)
è ancora un autovettore di A
con autovalore l .
In generale l'insieme degli autovettori di A con
autovalore l, unito al vettore zero,
coincide con Ker(A- l
I) che si dice autospazio di A relativo a l.
Definizione Due matrici A e B si dicono simili se esiste C invertibile tale che
A=C-1BC.
Esercizio Provare che la similitudine è una relazione di equivalenza.
Lemma
Due matrici simili hanno lo stesso polinomio caratteristico.
Dimostrazione
Siano A e B simili, quindi esiste C tale che
A=C-1BC.
Allora
pA(t)=det(A-tI)=det(C-1BC-tI)=
det(C-1(B-tI)C)=det(C-1)det(B-tI)det(C)=
det(B-tI)=pB(t).
Esercizi
- Provare che se A è una matrice 2x2 allora
pA(t)=t2-tr(A)t+det(A)
- Provare che lo spettro di una matrice triangolare è costituito dagli
elementi sulla diagonale.
Definizione Una matrice quadrata A si dice diagonalizzabile
se è simile ad una matrice diagonale.
Teorema Una matrice A è diagonalizzabile se e solo se
esiste una base di autovettori di A.
Dimostrazione Se A è diagonalizzabile allora esiste C invertibile tale che C-1AC=D con D diagonale. Moltiplicando a sinistra per C si ottiene
AC=CD
Se Ci è la i-esima colonna di C e
l i è l'i-esimo elemento diagonale di D l'equazione precedente equivale a
ACi = l iCi per ogni i
e quindi le colonne di C formano la base richiesta di autovettori.
Viceversa se esiste una base di autovettori per A, definiamo C la matrice che ha come colonna i-esima l'i-esimo autovettore Ci .
Allora vale
ACi = l iCi per ogni i
da cui chiamando con D la matrice che ha
l 1,..., l n sulla diagonale segue
AC=CD
da cui C-1AC=D come volevamo.
Osservazione importante Il teorema precedente ammette una interpretazione a un livello più astratto. Infatti la matrice
di fA rispetto ad una base qualunque ha sempre la forma
C-1AC per una qualche matrice invertibile C (matrice di cambiamento di base dalla base canonica ad una base qualunque).
Sia {v1,...,vn} una base di autovettori per una applicazione lineare T:V ® V.
Allora
T(vi)= l ivi
In particolare
T(v1)= l 1v1+
0 v2+...0 vn
e quindi la prima colonna della matrice di T
rispetto a {v1,...,vn} è data da
In questo modo si vede che la matrice di T
rispetto a {v1,...,vn} è la matrice diagonale con elementi diagonali
{ l 1,...,
l n}.
Questo ragionamento è invertibile nel senso che se la matrice di T rispetto ad una certa base è diagonale allora tale base
è composta da autovettori.
Pertanto se A ammette una base di autovettori, il ragionamento precedente applicato
a T=fA mostra che per la matrice C di cambiamento di base
C-1AC è diagonale e quindi A è diagonalizzabile. Questa è una seconda dimostrazione
del teorema precedente (o meglio una interpretazione da un punto di vista diverso della dimostrazione già vista).
Osservazione Se A diagonalizzabile è simile a D diagonale,
allora sulla diagonale di D appaiono gli autovalori di A. Infatti A e D hanno lo steso polinomio caratteristico.
Il primo esempio di matrice non diagonalizzabile.
Osservazione facoltativa
- Cn è costituito per definizione da n-ple di numeri complessi. Per approfondimenti rimandiamo al libro di Abate. In Cn
sono definite le operazioni di somma e di prodotto per uno scalare (che in questo caso può essere un numero complesso e non soltanto reale). Cn risulta uno spazio vettoriale
sul campo C dei numeri complessi. Si possono definire matrici a coefficienti complessi, e le operazioni tra matrici si definiscono analogamente al caso reale. In particolare è ben definito il determinante di una matrice quadrata. Tutta la parte dell'algebra lineare che non fa uso di lunghezze e del concetto di ortogonalità
si estende al caso complesso. In particolare una matrice quadrata a coefficienti complessi è invertibile se e solo se il suo determinante è non nullo.
-
L'insieme delle radici complesse del polinomio caratteristico di A si chiama lo spettro complesso di A. La dimostrazione precedente
mostra che l ÎC è radice del polinomio
caratteristico di A se e solo se esiste v ÎCn
tale che Av= l v. Un tale v si dice autovettore (complesso) di A con autovalore (complesso) = l .
Esercizi
- Provare che una matrice 2x2 ha due autovalori reali se e solo se (tr A)2-4det(A) > 0.
- Provare che una matrice 2x2 ha due autovalori distinti se e solo se (tr A)2-4det(A)¹ 0.
- Provare che una matrice 2x2 simmetrica ha sempre
autovalori reali. Il risultato è vero per matrici simmetriche nxn
Corollario Una matrice A ammette una base ortonormale di autovettori se e solo se esiste C ortogonale tale che
C-1AC è diagonale.
Dimostrazione Segue dalla dimostrazione
del teorema, infatti le colonne di C costituiscono la base di autovettori, se tale base è ortonormale
allora C è ortogonale per la proposizione.
Corollario
Se una matrice A ammette una base ortonormale di autovettori
allora è simmetrica.
Dimostrazione
Ricordiamo che se C è ortogonale vale C-1=tC.
Quindi da C-1AC=D segue
A=CDC-1=CDtC
da cui
tA=t(CDtC)=
t(sup>tC)(tD)tC=
CDtC=A
come volevamo.
Il teorema spettrale afferma che nel corollario precedente vale anche il viceversa.
Lemma Se una matrice A è simmetrica allora tutte
le radici del suo polinomio caratteristico sono reali.
Dimostrazione (facoltativa)
Teorema spettrale
Una matrice A è simmetrica se e solo se ammette una base ortonormale di autovettori. In particolare ogni matrice simmetrica è diagonalizzabile.
Dimostrazione
Sia A simmetrica nxn. Per il corollario
è sufficiente dimostrare che esiste C ortogonale tale che
C-1AC=D diagonale.
Dimostriamo questa affermazione per induzione su n.
Per n=1 l'enunciato è ovvio prendendo C=[1].
Sia vera l'affermazione per matrici simmetriche (n-1)x(n-1).
Per il lemma precedente esiste l
autovalore reale di A.
Quindi esiste v1 tale che
Av1 = l
v1 .
Posso supporre v1 di lunghezza 1 (dividendo per la sua lunghezza
per l'osservazione.
Completiamo v1 ad una base di Rn,
applicando l'algoritmo di Gram-Schmidt trovo
{v1,..., vn } base ortonormale di
Rn. Sia O la matrice ortogonale che ha
vi come i-esima colonna.
Allora O e1=v1.
Pertanto la prima colonna di O-1AO è
(O-1AO)e1=
O-1A(Oe1)=O-1(Av1)=
O-1( l
v1)= l (O-1 v1)= l e1 .
Inoltre O-1AO=tOAO è simmetrica e quindi abbiamo
|
O-1AO= |
é
ê
ê
ê
ê
ê
ê
ê
ë
|
| |
ù
ú
ú
ú
ú
ú
ú
ú
û
|
|
|
dove A' é una matrice simmetrica (n-1)x(n-1).
Per ipotesi induttiva esiste C' ortogonale (n-1)x(n-1) tale che
e quindi posto
|
C¢¢: = |
é
ê
ê
ê
ê
ê
ê
ê
ë
|
| |
ù
ú
ú
ú
ú
ú
ú
ú
û
|
|
|
segue
|
(C¢¢)-1O-1AOC¢¢= |
é
ê
ê
ê
ê
ê
ê
ê
ë
|
| |
ù
ú
ú
ú
ú
ú
ú
ú
û
|
|
|
e quindi C:=OC¢¢ é la matrice ortogonale cercata.
Esercizio Provare che autovettori di una matrice simmetrica corrispondenti ad autovalori distinti sono ortogonali.
Affrontiamo adesso il problema della diagonalizzabilità di una matrice non necessariamente simmetrica.
Teorema
Siano {v1,...,vn} autovettori di A
corrispondenti ad autovalori distinti. Allora
{v1,...,vn} sono indipendenti.
Dimostrazione Ragioniamo per induzione su n. Il caso n=1 è banale. Consideriamo la combinazione lineare
a1v1+ ...+anvn=0  ace;(*) Moltiplicando per A segue
a1Av1+ ...+anAvn=0
da cui
a1 l1
v1+ ...+an ln vn=0  ace;(**)
Moltiplicando (*) per l1
e sottraendo da (**) segue
(l2
-l1)a2v2+
...+
(ln
-l1)
anvn=0
Per ipotesi induttiva
{v2,...,vn} sono indipendenti. Quindi
(li
-l1)ai=0
per i=2,...,n. Siccome
(li
-l1)Î 0
segue ai=0
per i=2,...,n. Sostituendo in (*) si ottiene anche a1=0
come volevamo.
Definizione La molteplicità algebrica di un autovalore di A
è la sua molteplicità come radice del polinomio caratteristico pA.
Definizione La molteplicità geometrica di un autovalore l
è la dimensione dell'autospazio Ker(A-lI).
Teorema
Per ogni autovalore la sua molteplicità geometrica
è minore od uguale alla sua molteplicità algebrica .
Dimostrazione Sia k la molteplicità geometrica
di l. Sia
{v1,...,vk} una base di
Ker(-lI). Completo ad una base di
Rn. La matrice di fA rispetto a questa base è
dove Ik è la matrice identità kxk.
Tale matrice è simile ad A e quindi il suo polinomio caratteristico è uguale a quello di A. Sviluppando successivamente rispetto alle prime k colonne il determinante
che definisce il polinomio caratteristico si ottiene che
(l-t)k divide pA
e quindi la tesi.
Criterio necessario e sufficiente di diagonalizzabilità
Una matrice A è diagonalizzabile se e solo se
- Tutti gli autovalori di A sono reali
- Per ogni autovalore la sua molteplicità geometrica
è uguale alla sua molteplicità algebrica .
Traccia della dimostrazione (facoltativa)
Se A è diagonalizzabile è facile verificare che le due condizioni sono soddisfatte (sulla sua forma diagonale). Viceversa supponiamo che le due condizioni siano soddisfatte e siano
l1,...,
lp gli autovalori di A nxn.
Sia k(i) la molteplicità di li. Considero una base {vi1,...,vik(i)} dell'autospazio Ker(A-liI). Affermo che l'unione di queste basi
{v11,...,v1k(1),...,vp1,...,vpk(p)} è una base di autovettori di A.
Il numero di questi autovettori è k(1)+...+k(p)=n
(perchè la somma delle molteplicità algebriche delle radici
è uguale al grado del polinomio).
Quindi è sufficiente dimostrare che tali autovettori sono indipendenti. La verifica di questo fatto segue
dal teorema ed è lasciata al lettore.
Corollario Una matrice nxn con n autovalori reali distinti
è diagonalizzabile.
DimostrazioneLa molteplicità algebrica di ogni autovalore è 1. Quindi dal
teorema abbiamo
0< molteplicità geometrica £
1 da cui per ogni autovalore
molteplicità geometrica = molteplicità algebrica =1
e dal teorema precedente segue la tesi.
Esercizio * Sia {l1
, ..., ln
} lo spettro complesso di A nxn. Provare che
traccia A=l1+
...+ln
det A=l1
...ln
Suggerimento: dato il polinomio
xn+an-1 xn-1+...a0
vale che an-1 è uguale a meno la somma delle radici,
mentre a0 è uguale a (-1)n per
il prodotto delle radici.
Calcolo delle potenze di una matrice diagonalizzabile
Sia A una matrice diagonalizzabile. Pertanto se le colonne di C formano una base di autovettori,
abbiamo A=CDC-1. Segue
A2=(CDC-1)(CDC-1)=CD(C-1C)DC-1=
CD2C-1
e più in generale si vede allo stesso modo che
Ak = CDkC-1
Il calcolo di Dk è immediato, si tratta ancora di una matrice diagonale i cui elementi
sono le potenze k-esime degli elementi di D.
Per illustrare questo calcolo concludiamo un esempio che era stato lasciato in sospeso.
Sia
Nell'esempio avevamo p=0,95, q=0,99. Ci proponiamo di calcolare le potenze Ak
diagonalizzando A. Gli autovalori di A sono 1 e p+q-1 con autovettori corrispondenti
rispettivamente
.
Posto
e
segue l'uguaglianza
da cui
|
Ak=CDkC-1= |
1
p+q-2
|
|
é
ê
ê
ê
ë
|
| |
ù
ú
ú
ú
û
|
· |
é
ê
ê
ê
ë
|
| |
ù
ú
ú
ú
û
|
· |
é
ê
ê
ê
ë
|
| |
ù
ú
ú
ú
û
|
|
|
É significativo notare che quando k® +¥ allora Ak tende a
quindi un qualunque vettore colonna
(a, b) tende se moltiplicato per Ak con k grande al vettore colonna
che é un multiplo del primo autovettore.
Questa distribuzione puó essere pensata come il punto di equilibrio del sistema dinamico.
a+b rappresenta la popolazione totale che si distribuisce secondo le proporzioni 1-q e 1-p.