Research interests




I'm mainly concerned with theoretical computer science (formal language theory), discrete mathematics and enumerative and algebraic combinatorics. More specifically, some topics I've worked on in the past, I'm presently working on, and I plan to work on in the near future are the following.


Umbral calculus

It is a technique which goes back to the work of Sylvester, Bell, Blissard and others; its rigorous mathematical foundation is given to Gian-Carlo Rota and is described ina series of papers appeared starting from the mid '60.

An umbral calculus over infinite coefficient fields of positive characteristic, Computers and Mathematics with Applications, 41 (2001) 1099-1108.
One of the possible presentation of the umbral calculus, namely finite operator calculus, is extended to the case of an infinite coefficient field of positive characteristic. All the main classical notions are suitably modified and some new concept is introduced as "the right one" to work with in this theory.

Polynomial rings in which delta operators are derivations, European Journal of Combinatorics, 22 (2001) 1059-1064.
Given a delta operator, a suitable multiplication is defined so to make the vector space of one-variable polynomials an algebra in which such a delta operator is a derivation (in the algebraic meaning). The derivation algebra obtained this way turns out to be isomorphic to the usual derivation algebra of polynomials (where the derivation is D). Then a complete classification of the isomorphisms between such algebras is provided.


Poset and lattice theory

A combinatorial representation for a special class of complete distributive lattices (with Giorgio Nicoletti), Annals of Combinatorics, 5 (2001) 285-304.
A class of infinite distributive lattices for which it is possible to prove a Birkhoff-like representation theorem (i.e. using combinatorial tools only, without the help of any topological structure) is determined.

On derivations of lattices, Pure Mathematics and Applications, 12 (2001) 365-382.
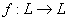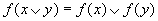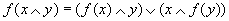Given a lattice L, a derivation is a function having the two following properties: (i) , and (ii). Some properties of these functions are studied, as well as some combinatorial, algebraic and geometric applications.

Lattices of lattice paths (with Renzo Pinzani), Journal of Statistical Planning and Inference, 135 (2005) 77-92.
A natural partial order on several classes of lattice path is considered, and a necessary and sufficient condition is given to decide if a specific poset of paths is in fact a distributive lattice (with coordinatewise meet and join). In particular, the case of the lattices of Dyck paths is analyzed in greater detail: a recursive construction of these lattices is provided.

A distributive lattice structure connecting Dyck paths, noncrossing partitions and 312-avoiding permutations (with Elena Barcucci, Antonio Bernini and Maddalena Poneti), Order, 22 (2005) 311-328.
The natural distributive lattice structure of Dyck paths described in Lattices of lattice paths (with Renzo Pinzani), Journal of Statistical Planning and Inference, 13 5 (2005) 77-92 is transferred here to noncrossing partitions and 312-avoiding permutations by means of more or less classical bijections. In particular, it is shown that the resulting structure on 312-avoiding permutations coincides with the one induced by the (strong) Bruhat order, proving in this way that this subposet of the symmetric group is more precisely a distributive lattice. Among other things, in the last section of the paper a combinatorial formula expressing Bell numbers in terms of natural parameters on Dyck paths is provided.

Some order-theoretic properties of the Motzkin and Schröder families (with Antonio Bernini), Australasian Journal of Combinatorics, 39 (2007) 259-272.
The results obtained in A distributive lattice structure connecting Dyck paths, noncrossing partitions and 312-avoiding permutations (with Elena Barcucci, Antonio Bernini and Maddalena Poneti), Order, 22 (2005) 311-328 are transferred on Motzkin and Schröder paths. In particular, it is shown that the classes of permutations simultaneously avoiding the generalized patterns 3-12 and k-(k-1)(k-2)···21 are distributive lattices with the order induced by the strong Bruhat order (for every k greater than 1).

Some combinatorics related to central binomial coefficients: Grand-Dyck paths, coloured noncrossing partitions and signed pattern avoiding permutations, Graphs and Combinatorics, 26 (2010) 51-70.
Enumerative and order-theoretic properties of some combinatorial structures counted by central binomial coefficients are studied. In particular, some new bijections between Grand-Dyck paths and coloured pattern avoiding permutations are determined. Moreover, it is shown that the lattices of Grand-Dyck paths of fixed length are isomorphic to certain subposets of the (strong) Bruhat order on coloured permutations which avoid specific (coloured) patterns.

Lattices of paths: representation theory and valuations (with Emanuele Munarini), Journal of Combinatorics, 2 (2011) 265-292.
Some combinatorial properties of certain classes of lattices of paths are studied, namely some simple representation results for Dyck-like paths are provided, and the Euler characteristic of Dyck, Motzkin and Schröder lattices is computed. Moreover, a combinatorial interpretation of the Euler characteristic in terms of tunnels is provided in the above mentioned cases.

The Möbius function of the consecutive pattern poset (with Antonio Bernini and Einar Steingrimsson), Electronic Journal of Combinatorics, 18(1) (2011) #P146 (12 pp.).
The set of all permutations forms a poset with respect to the consecutive pattern containment (i.e. σ is less than or equal to π when there exists a set of consecutive elements of π which is order isomorphic to σ). We study the Möbius function of such a poset, giving a (polynomial time) recursive procedure to compute it. In particular, we show that such a function only takes the values -1,0 and 1.

Catalan lattices on series parallel interval orders (with Filippo Disanto, Renzo Pinzani and Simone Rinaldi), in: Folkert Müller-Hoissen, Jean Pallo e Jim Stasheff (Eds.), Associahedra, Tamari Lattices and Related Structures (Tamari Festschrift), Progress in Mathematics, 299, Birkhäuser, Basel, 2012, pp. 323-338. 
We propose a unified setting to describe the classical Dyck and Tamari lattices in terms of series parallel interval orders. Then such structures are compared with the strong and weak Bruhat orders on 312-avoiding permutations.

Unimodality and Dyck paths, Journal of Combinatorial Mathematics and Combinatorial Computing, 87 (2013) 65-79.
We propose a presumably new approach to a 20 years old problem. In the stated formulation, it consists of proving or disproving that Dyck lattices are rank-unimodal. Unfortunately we are not able to give an answer to this question; however we provide a partition of Dyck lattices into saturated chains (based on a well known ECO construction) and study a related family of polynomials which may be useful to tackle the problem. Finally we suggest a systematic approach to the study of unimodality of succession rules.

Pattern-avoiding Dyck paths (with Antonio Bernini, Renzo Pinzani e Julian West), Discrete Mathematics and Theoretical Computer Science Proceedings, AS (2013) 713-724.
The Dyck pattern poset (with Axel Bacher, Antonio Bernini,Benjamin Gunby, Renzo Pinzani, Julian West), journal version, Discrete Mathematics, 321 (2014) 12-23.
The notion of pattern of a permutation is adapted to Dyck paths, giving rise to a poset of Dyck paths analogous to the permutation pattern poset. Given a Dyck path, the number of paths covering it and the number of paths it covers are determined. Moreover some classes of Dyck paths avoiding a single pattern are enumerated. We also suggest a recursive approach to the enumeration of classes of paths avoiding any single pattern, from which we can deduce an algorithm to compute the generating function, and we determine the asymptotic behavior of such classes of paths. Finally some open problems concerning the structure of the Dyck pattern poset are proposed, such as the computation of the Möbius function, the enumeration of chains and the study of the notion of Wilf-equivalence.

Enumeration of edges in some lattices of paths (with Emanuele Munarini), Journal of Integer Sequences, 17 (2014) Article 14.1.5 (22 pp.).
We enumerate covering relations in some classes of lattices of paths, such as Dyck, Motzkin and Schröder. Moreover we introduce and compute the Hasse index the the lattices under consideration. Finally we provide a general formula for the enumeration of covering relations in a generic Young lattice, which can be naturally interpreted as a lattice of path.

Enumeration of chains and saturated chains in Dyck lattices (with Emanuele Munarini), Advances in Applied Mathematics, 62 (2015) 118-140.
A general formula for the enumeration of saturated chains in Dyck lattices is described. Such a formula is then applied to determine both the generating function and a closed form for the number of saturated chains of length 2 and 3. Finally the notion of Hasse index introduced in Enumeration of edges in some lattices of paths (with Emanuele Munarini), Advances in Applied Mathematics, 62 (2015) 118-140 is suitably generalized.

Greedy algorithms and poset matroids, Journal of Discrete Algorithms, 29 (2014) 21-26.
An analog of Edmonds-Rado theorem for poset matroids (in the sense of Barnabei, Nicoletti and Pezzoli) is proved. The result is then applied to find a generalization of Kruskal algorithm (to determine the minimum spanning subtree of a weighted graph) to abstract simplicial complexes.

Dyck algebras, interval temporal logic and posets of intervals, SIAM Journal on Discrete Mathematics, 30 (2016) 1918-1937.
The Heyting algebra structure canonically associated with the finite distributive structure of Dyck lattices is investigated. The resulting Heyting algebras are called Dyck algebras. A geometric description of the relative pseudocomplement is given, and a logic-theoretic interpretation of such algebras in terms of a fragment of the interval temporal logic of Halpern and Shoham is provided.

A partial order structure on interval orders (con Filippo Disanto e Simone Rinaldi), Utilitas Mathematica, 102 (2017) 135-147.
The set of interval orders of a given size is endowed with a distributive lattice structure which generalizes the classical Tamari order (on the ground set of series parallel interval orders).

Vincular pattern posets and the Möbius function of the quasi-consecutive pattern poset (with Antonio Bernini), Annals of Combinatorics, 21 (2017) 519-534.
After having defined a poset structure on finite permutations in terms of containment of patterns of fixed type, we specifically investigate the case of quasi-consecutive patterns, where, by definition, a permutation t contains the quasi consecutive pattern s whenever s occurs in t as a consecutive pattern, except at most for the first and the second entries. In particular, we study the Möbius function of the resulting poset, and we compute it in the case of intervals whose bottom permutation occurs precisely once in the top permutation.

Enumerative results on the Schröder pattern poset (with Lapo Cioni), in: Dennunzio A., Formenti E., Manzoni L., Porreca A. (eds) Cellular Automata and Discrete Complex Systems, AUTOMATA 2017, Lecture Notes in Computer Science, 10248 (2017), Springer, Cham,
Analogously to Pattern-avoiding Dyck paths (con Antonio Bernini, Renzo Pinzani e Julian West), Discrete Mathematics and Theoretical Computer Science Proceedings, AS (2013) 713-724, we investigate the notion of pattern in a Schröder path from an enumerative point of view. Specifically, we find formulas for the number of Schröder paths covering/covered by a given path (in terms of natural parameters on paths) and we enumerate some classes of Schröder paths avoiding a single path.

Research projects


ECO method

This is a methodology used in enumerative and bijective combinatorics developed by a group of researchers in the "Dipartimento di Sistemi e Informatica" of the University of Firenze in the early 90's (including Renzo Pinzani, Elena Barcucci, Alberto Del Lungo and Elisa Pergola). Given a class of combinatorial objects and a notion of size on it, the ECO method allows to effectively construct a set of objects of size n+1 starting from an object of size n. This is performed in such a way that each object has a unique father (i.e., is produced by a unique object). Thus, for every n, a partition of the objects of size n is naturally defined. The above mentioned construction can often be described by means of a suitable succession rule, and this offers the possibility of enumerating the class of object under consideration in terms of several parameters

A linear operator approach to succession rules (with Renzo Pinzani), Linear Algebra and Its Applications, 348 (2002) 231-246.
Every succession rule is represented by means of a suitable linear operator (calledrule operator) in the vector space of one-variable polynomials, and all the enumerative information hidden in the rule are rediscovered in terms of such an operator. Several examples are considered, and the usefulness of our approach is confirmed by determining a standard form for any given succession rule.

An algebraic characterization of the set of succession rules (with Elisa Pergola, Renzo Pinzani and Simone Rinaldi), Theoretical Computer Science, 281 (2002) 351-367.
An algebra of succession rules in introduced in such a way that, given two succession rules, we are able to determine the form of a succession rule whose associated numerical sequence is related to the numerical sequences associated with the starting succession rules by means of the applications of several algebraic operations (such as sum, convolution, Hadamard product, etc.). To prove almost all the theorems the technique of rule operators turns out to be extremely useful.

Jumping succession rules and their generating functions (with Elisa Pergola, Renzo Pinzani and Simone Rinaldi), Discrete Mathematics, 271 (2003) 29-50.
We define the notion of jumping succession rule: it is a succession rule such that each node of its generating tree produces its sons not exclusively at the successive level, but it can possibly produce sets of sons at several different levels. Here it is studied the situation in which the sets of sons produced at the various levels are described by means of the same succession rule. In this case, complete enumerative results are provided (that is, the numerical sequence associated with the jumping succession rule is expressed in terms of the numerical sequence associated with the starting succession rule).

Enumerative results on integer partitions using the ECO method (with Renzo Pinzani and Simone Rinaldi), Mathematics and Computer Science, III (Wien, 2004), Trends in Mathematics, Birkhauser, Basel, pp.25-36.
A succession rule with an infinite number of jumps is defined for the class of integer partitions. Some classical results are rediscovered using such a succession rule. Some applications concerns lecture hall partitions (for which a possible new bijective proof of the fundamental theorem relating them to integer partitions into a finite number of odd parts is conjectured) and integer partitions contained inside a generalized hook (for them we also provide a complete enumerative result).

Production matrices (with Emeric Deutsch and Simone Rinaldi), Advances in Applied Mathematics, 34 (2005) 101-122.
The notion of production matrix is introduced. This is the matrix counterpart of the notion of rule operator. As for rule operators, it is explained how to read inside the production matrix all the main enumerative information hidden in the associated succession rule. Moreover, we define suitable operations on production matrices which corresponds to several algebraic operations on the numerical sequences determined by the related succession rules.

Enumerating permutations avoiding three Babson-Steingrimsson patterns (with Antonio Bernini and Renzo Pinzani), Annals of Combinatorics, 9 (2005) 137-162.
The ECO method and a special graphical representation of permutations are used to enumerate all the class of permutations simultaneously avoiding three generalized patterns of length 3 and of type a-bc or ab-c, thus proving a series of conjectures by Claesson and Mansour.

Catalan-like numbers and succession rules (with Renzo Pinzani), Pure Mathematics and Applications, 16 (2005) 229-250.
An invertible linear transformation is defined such that, in a great amount of cases, translates an ECO matrix (i.e. the infinite matrix associated with a generating tree in such a way that the entry (n,k) gives the numer of labels (k) at level (n)) into an Aigner matrix whose associated Catalan-like numbers coincide with the numerical sequence determined by the starting ECO matrix. Several examples are provided and some special classes of succession rules are analyzed in greater detail (namely factorial and differential succession rules).

Some statistics on permutations avoiding generalized patterns (with Antonio Bernini and Mathilde Bouvel), Pure Mathematics and Applications, 18 (2007) 223-237.
The statistics "first/last entry" are studied for some classes of pattern avoiding permutations.

Production matrices and Riordan arrays (with Emeric Deutsch and Simone Rinaldi), Annals of Combinatorics, 13 (2009) 65-85.
The relationship between ECO matrix and Riordan arrays is investigated. In particular, the form of a production matrix in order to generate a Riordan (or exponential Riordan) ECO matrix is established. Moreover, we study some properties of production matrices associated with finite and rational succession rules. The paper is enriched by a vast gallery of examples.

Enumeration of some classes of words avoiding two generalized patterns of length three (with Antonio Bernini and Renzo Pinzani), Journal of Automata, Languages and Combinatorics, 14 (2009) 129-147.
The method we have applied in Enumerating permutations avoiding three Babson-Steingrimsson patterns (con Antonio Bernini e Renzo Pinzani), Annals of Combinatorics, 9 (2005) 137-162 to count pattern avoiding permutations is adapted to words. As an application, we enumerate several classes of words simultaneously avoiding two generalized patterns of length 3.

Mixed succession rules: the commutative case (with Silvia Bacchelli, Renzo Pinzani and Renzo Sprugnoli), Journal of Combinatorial Theory, Series A, 117 (2010) 568-582.
Generalizing Jumping succession rules and their generating functions (with Elisa Pergola, Renzo Pinzani e Simone Rinaldi), Discrete Mathematics, 271 (2003) 29-50, we study succession rules such that, in the associated generating tree, the nodes are allowed to produce their sons at several different levels according to different production rules. We consider the situation in which a node at level n produces a set of sons at level n+1 according to a certain production rule and a set of sons at level n+2 according to another (possibly different) production rule. In this case, if the rule operators associated with the two production rules commute, we are able to find a formula expressing the numerical sequence determined by the mixed rule in terms of enumerative parameters of the component rules. Some examples and combinatorial interpretations are provided to illustrate our theory.

ECO species (with Pierre Leroux), Séminaire Lotharingien de Combinatoire 61A (2010) Article B61Al, 23pp.
The notion of ECO species is introduced, in order to provide a formal description of an ECO construction and of a generating tree inside the theory of (linear) species. Some operations on ECO species are described and illustrated with examples.

Some applications arising from the interactions between the theory of Catalan-like numbers and the ECO method (with Elisa Pergola, Renzo Pinzani and Simone Rinaldi), Ars Combinatoria, 99 (2011) 109-128. 
Some combinatorial applications deriving from the use of the linear transformation connecting ECO matrices with Aigner matrices introduced in Catalan-like numbers and succession rules are described. The possibility of switching from one theory to the other allows in fact to tackle problems which are considered difficult in the context of one theory by simply translating them into equivalent statements of the other theory. Using this technique, we have defined a bijection between Grand-Dyck paths starting with an up step and coloured Motzkin paths having, more precisely, bicoloured horizontal steps, except for the horizontal steps lying on the x-axis, which can be tricoloured. Moreover, the same technique has provided a combinatorial interpretation for a "non-Sheffer" Aigner matrix, by means of a special class of coloured steep polyominoes.

Research projects

 

Enumerative and bijective combinatorics

Some bijective results about the area of Schröder paths (with Elisabetta Grazzini, Elisa Pergola and Simone Rinaldi), Theoretical Computer Science, 307 (2003) 327-335.
A combinatorial interpretation of the even-indexed terms of the sequence 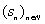, defined by the recurrence relation 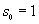, , 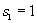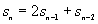is provided. Such a combinatorial interpretations involves the total area of elevated Schröder paths.

Enumeration of generalized hook partitions (with Simone Rinaldi), Integers, 5 (2005) #A29 (7 pp.).
The generating function of the class of integer partitions whose Ferrers diagrams is contained into both a generalized hook and the intersection of two generalized hooks is determined (recall that a generalized hook differs from a classical hook in the fact that the height and the width of the hook are positive integers possibly different from 1).

Combinatorial properties of Catalan pairs (con Filippo Disanto, Renzo Pinzani e Simone Rinaldi), Electronic Notes in Discrete Mathematics, 34 (2009) 429-433.
Catalan pairs: a relational-theoretic approach to Catalan numbers (con Filippo Disanto, Renzo Pinzani e Simone Rinaldi), journal version, Advances in Applied Mathematics, 45 (2010) 505-517.
The notion of a Catalan pair is introduced, aiming at providing a common language to many combinatorial interpretations of Catalan numbers. It is a pair (R,S) of strict partial order relations on the same set satisfying some specific axioms. After having proved some fundamental properties of Catalan pairs, as, for instance, the fact that they are enumerated by Catalan numbers (up to isomorphisms), some instances of interpretations of Catalan numbers are proposed for which it is quite easy to determine the associated Catalan pair. Next the posets associated with R and S are studied, and it is shown, among other things, that R uniquely determines the Catalan pair and that the poset determined by R can be described in terms of forbidden configurations. Finally, Catalan pairs for which R enjoys some specific properties are described (that is, when R determines a connected poset, or else a (possibly) distributive lattice), and the definition of a Catalan pair is slightly modified in order to define an analogous concept for other integer sequences, such as central binomial coefficients and Schröder numbers.

On the enumeration of d-minimal permutations (with Mathilde Bouvel), Discrete Mathematics and Theoretical Computer Science, 15(2) (2013) 33-48.
We suggest a possible approach to the study (and in particular the enumeration) of minimal permutations having d descents by means of a certain family of skew Young tableaux. Such an approach allows to deduce a general formula in terms of sums of determinants. We also propose a generalization of the above mentioned family of tableaux, which leads, among other things, to Eulerian numbers.

Schröder partitions and Schröder tableaux, in: Lipták Z., Smyth W. (eds) Combinatorial Algorithms. Lecture Notes in Computer Science, 9538 (2016), Springer, Cham, pp. 161-172.
Schröder partitions, Schröder tableaux and weak poset patterns, journal version, submitted (2016).
The notions of Schröder shape and Schröder tableau are introduced, which provide a sort of analog of the classical notions of Young shape and Young tableau. After a brief investigation of some simple properties of the poset of Schröder shapes, an algorithm which is an analog of the Robinson-Schenstd correspondence for standard Young tableaux is described, and some of its properties are studied. Finally, a connection between Schröder tableaux and interval orders is proposed, which is based on the (not so well known) notion of weak poset pattern. 

Research projects

 

 

Further research projects