Interessi di ricerca




Mi occupo principalmente di informatica teorica (teoria dei linguaggi formali), matematica discreta e combinatoria enumerativa e algebrica. Più specificamente, gli argomenti su cui ho lavorato in passato, sto lavorando al presente, e intendo lavorare in futuro sono i seguenti.


Calcolo umbrale

Si tratta di una tecnica di calcolo le cui radici affondano nell'opera di Sylvester, Bell, Blissard e altri, e la cui sistemazione teorica rigorosa è dovuta a Gian-Carlo Rota ed è contenuta in una serie di lavori apparsi a partire dalla metà degli anni '60.

An umbral calculus over infinite coefficient fields of positive characteristic, Computers and Mathematics with Applications, 41 (2001) 1099-1108.
Viene analizzata una delle possibili presentazioni del calcolo umbrale, segnatamente quella come calcolo operatoriale, in cui vengono studiate le proprietà di particolari classi di successioni polinomiali su un campo di caratteristica 0 nonchè di speciali classi di operatori lineari agenti su tali polinomi. Nell'articolo viene proposta una possibile traduzione di tale versione del calcolo umbrale nel caso in cui il campo dei coefficienti sia infinito e abbia caratteristica diversa da 0. Tutti i principali concetti classici vengono opportunamente adattati e qualche nuova nozione viene introdotta come particolarmente naturale in questo ambito.

Polynomial rings in which delta operators are derivations, European Journal of Combinatorics, 22 (2001) 1059-1064.
Dato un operatore delta, viene definito un opportuno prodotto che rende lo spazio vettoriale dei polinomi un'algebra in cui tale operatore delta è una derivazione (in senso algebrico). L'algebra con derivazione così ottenuta risulta isomorfa all'algebra con derivazione canonica dei polinomi (quella cioè in cui la derivazione è quella classica). Viene poi proposta una classificazione completa di tutti gli isomorfismi fra tali algebre.


Teoria dei poset e dei reticoli

A combinatorial representation for a special class of complete distributive lattices (con Giorgio Nicoletti), Annals of Combinatorics, 5 (2001) 285-304.
Viene individuata una classe di reticoli distributivi infiniti per i quali è possibile dimostrare un teorema di rappresentazione "alla Birkhoff", vale a dire utilizzando solo concetti e nozioni puramente combinatorie, senza ricorrere all'ausilio di strutture topologiche.

On derivation of lattices, Pure Mathematics and Applications, 12 (2001) 365-382.
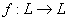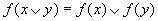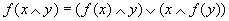Dato un reticolo L, si chiama derivata di L una funzione avente le seguenti due proprietà: (i) , e (ii). Vengono studiate alcune proprietà di tali funzioni, nonchè applicazioni di tipo combinatorico, algebrico e geometrico.

Lattices of lattice paths (con Renzo Pinzani), Journal of Statistical Planning and Inference, 135 (2005) 77-92.
Viene definito un ordine naturale su diverse classi di cammini nel piano, e viene fornita una condizione necessaria e sufficiente per stabilire se i poset definiti da una specifica classe di cammini sono in realtà reticoli distributivi (con sup e inf definiti coordinata per coordinata). Viene analizzato in particolare il caso dei reticoli individuati dai cammini di Dyck, per i quali viene descritto un algoritmo che permette di costruire tali reticoli ricorsivamente.

A distributive lattice structure connecting Dyck paths, noncrossing partitions and 312-avoiding permutations (con Elena Barcucci, Antonio Bernini e Madalena Poneti), Order, 22 (2005) 311-328.
La struttura naturale di reticolo distributivo dei cammini di Dyck descritta in Lattices of lattice paths (con Renzo Pinzani), Journal of Statistical Planning and Inference, 13 5 (2005) 77-92 viene trasportata sulle partizioni noncrossing e sulle permutazioni che evitano il motivo 312 utilizzando biiezioni più o meno classiche fra tali strutture. Si dimostra, in particolare, che la struttura risultante sulle permutazioni che evitano 312 coincide con la restrizione dell'ordine (forte) di Bruhat, mostrando in tal modo che tale sottoposet del gruppo simmetrico è più precisamente un reticolo distributivo. Tra le altre cose, nell'ultima parte dell'articolo si da anche un'espressione combinatoria dei numeri di Bell in termini di parametri naturali sui cammini di Dyck.

Some order-theoretic properties of the Motzkin and Schröder families (con Antonio Bernini), Australasian Journal of Combinatorics, 39 (2007) 259-272.
I risultati di A distributive lattice structure connecting Dyck paths, noncrossing partitions and 312-avoiding permutations (con Elena Barcucci, Antonio Bernini e Madalena Poneti), Order, 22 (2005) 311-328 vengono trasferiti al caso dei cammini di Motzkin e di Schröder. In particolare, viene dimostrato che le permutazioni che evitano simultaneamente i motivi generalizzati 3-12 e k-(k-1)(k-2)···21 sono reticoli distributivi rispetto all'ordine di Bruhat forte (per ogni k maggiore di 1).

Some combinatorics related to central binomial coefficients: Grand-Dyck paths, coloured noncrossing partitions and signed pattern avoiding permutations, Graphs and Combinatorics, 26 (2010) 51-70.
Vengono studiate proprietà enumerative e d'ordine di alcune strutture combinatorie contate dai coefficienti binomiali centrali. In particolare, vengono determinate nuove biiezioni fra cammini di Grand-Dyck e specifiche classi di permutazioni colorate a motivo escluso e si dimostra che i reticoli dei cammini di Grand-Dyck di lunghezza fissata sono isomorfi a determinati sottoinsiemi parzialmente ordinati dell'ordine di Bruhat sulle permutazioni colorate che escludono specifici motivi, anch'essi colorati.

Lattices of paths: representation theory and valuations (con Emanuele Munarini), Journal of Combinatorics, 2 (2011) 265-292.
Vengono studiate alcune proprietà combinatorie di particolari classi di reticoli di cammini, più precisamente vengono forniti alcuni semplici risultati di rappresentazione per le classi di cammini Dyck-like e viene calcolata la caratteristica di Eulero in particolare dei reticoli dei cammini di Dyck, Motzkin e Schröder. Inoltre, per la caratteristica di Eulero dei reticoli di cui sopra, viene anche fornita un'interessante interpretazione combinatoria in termini di tunnel.

The Möbius function of the consecutive pattern poset (con Antonio Bernini e Einar Steingrimsson), Electronic Journal of Combinatorics, 18(1) (2011) #P146 (12 pp.).
L'insieme di tutte le permutazioni è un insieme parzialmente ordinato rispetto all'inclusione di motivi consecutivi (vale a dire σ è minore o uguale a π quando esiste un segmento di elementi consecutivi di π ordinatamente isomorfo a σ). Viene studiata la funzione di Möbius di tale insieme parzialmente ordinato, fornendo una procedura ricorsiva (avente tempo polinomiale) per calcolarla. In particolare, si mostra che i valori che tale funzione può assumere sono soltanto -1,0 e 1.

Catalan lattices on series parallel interval orders (con Filippo Disanto, Renzo Pinzani e Simone Rinaldi), in: Folkert Müller-Hoissen, Jean Pallo e Jim Stasheff (Eds.), Associahedra, Tamari Lattices and Related Structures (Tamari Festschrift), Progress in Mathematics, 299, Birkhäuser, Basel, 2012, pp. 323-338.
Viene proposto un linguaggio per descrivere i classici reticoli di Dyck e Tamari in termini di series parallel interval orders. Tali strutture vengono poi anche messe in relazione con gli ordini di Bruhat (forte e debole) sulle permutazioni che evitano il motivo 312.

Unimodality and Dyck paths, Journal of Combinatorial Mathematics and Combinatorial Computing, 87 (2013) 65-79.
Viene proposto un approccio presumibilmente nuovo ad un problema che resiste da più di 20 anni. Nella formulazione proposta, si tratta di dimostrare o confutare il fatto che i reticoli di Dyck sono unimodali rispetto al rango. Purtroppo la questione non viene risolta, ma si presenta una partizione dei reticoli di Dyck in catene saturate (basato su una nota costruzione ECO) e si studia una famiglia di polinomi ad essa associata che potrebbero essere utili ad affrontare il problema. Infine viene suggerito un approccio sistematico allo studio dell'unimodalità delle regole di successione.

Pattern-avoiding Dyck paths (con Antonio Bernini, Renzo Pinzani e Julian West), Discrete Mathematics and Theoretical Computer Science Proceedings, AS (2013) 713-724.
The Dyck pattern poset (con Axel Bacher, Antonio Bernini, Benjamin Gunby, Renzo Pinzani, Julian West), versione estesa, Discrete Mathematics, 321 (2014) 12-23.
La nozione di motivo in una permutazione viene adattata al caso dei cammini di Dyck, dando origine a un insieme parzialmente ordinato di cammini di Dyck analogo a quello delle permutazioni. Dato un cammino di Dyck viene determinato il numero di cammini che esso copre e da cui è coperto. Inoltre vengono enumerate alcune classi di cammini di Dyck che evitano un singolo motivo. Viene anche suggerito un approccio ricorsivo al conteggio di classi di cammini che evitano un qualunque singolo motivo, dal quale si può dedurre un algoritmo per calcolarne la funzione generatrice, e viene determinato il comportamento asintotico ti tali classi di cammini. Infine vengono proposti alcuni problemi aperti riguardanti la struttura di ordine parziale introdotta, quali il calcolo della funzione di Möbius, il conteggio delle catene e lo studio della nozione di Wilf-equivalenza.

Enumeration of edges in some lattices of paths (con Emanuele Munarini), Journal of Integer Sequences, 17 (2014) Article 14.1.5 (22 pp.).
Vengono enumerate le relazioni di copertura in alcune classi di reticoli di cammini, quali Dyck, Motzkin, Schröder. Viene poi introdotto e calcolato l'indice di Hasse dei reticoli considerati. Infine viene fornita una formula generale per l'enumerazione delle relazioni di copertura in un generico reticolo di Young, che può essere interpretato in modo naturale come reticolo di cammini.

Enumeration of chains and saturated chains in Dyck lattices (con Emanuele Munarini), Advances in Applied Mathematics, 62 (2015) 118-140.
Viene descritta una formula generale per il conteggio delle catene saturate nei reticoli di Dyck. Tale formula viene poi utilizzata per determinare la funzione generatrice e una forma chiusa per il numero di catene saturate di lunghezza 2 e 3. Viene poi generalizzato il concetto di indice di Hasse introdotto in Enumeration of edges in some lattices of paths (con Emanuele Munarini), Advances in Applied Mathematics, 62 (2015) 118-140.

Greedy algorithms and poset matroids, Journal of Discrete Algorithms, 29 (2014) 21-26.
Viene dimostrato un analogo del teorema di Edmonds-Rado nel contesto delle matroidi su insiemi parzialmente ordinati (secondo la definizione di Barnabei, Nicoletti e Pezzoli). Il risultato ottenuto viene poi utilizzato per ricavare una generalizzazione dell'algoritmo di Kruskal (per determinare il minimo albero ricoprente di un grafo pesato) al caso dei complessi simpliciali astratti.

Dyck algebras, interval temporal logic and posets of intervals, SIAM Journal on Discrete Mathematics, 30 (2016) 1918-1937.
Viene studiata la struttura di algebra di Heyting canonicamente associata alla struttura di reticolo distributivo finito dei reticoli di Dyck. Le algebre di Heyting risultanti sono dette algebre di Dyck. Più specificamente, viene fornita una descrizione geometrica dell'operazione di pseudocomplemento relativo e un'interpretazione logica di tali algebre mediante un determinato frammento della logica temporale degli intervalli di Halpern e Shoham.

A partial order structure on interval orders (con Filippo Disanto e Simone Rinaldi), Utilitas Mathematica, 102 (2017) 135-147.
L'insieme degli interval orders di fissata taglia viene dotato di una struttura di reticolo distributivo che generalizza il classico ordine di Tamari (sull'insieme dei series parallel interval orders).

Vincular pattern posets and the Möbius function of the quasi-consecutive pattern poset (con Antonio Bernini), Annals of Combinatorics, 21 (2017) 519-534.
Dopo aver definito una struttura di insieme parzialmente ordinato sull'insieme delle permutazioni finite in termini di contenimento di motivi di determinato tipo, si analizza il caso delle motivi quasi consecutivi, ove per definizione una permutazione t contiene il motivo quasi consecutivo s quando s compare in t come motivo consecutivo, eccetto al più per la prima e la seconda lettera. In particolare si studia la funzione di Möbius dell'insieme parzialmente ordinato risultante, risolvendo completamente il caso degli intervalli in cui la permutazione minima compare esattamente una volta nella permutazione massima.

Enumerative results on the Schröder pattern poset (con Lapo Cioni), in: Dennunzio A., Formenti E., Manzoni L., Porreca A. (eds) Cellular Automata and Discrete Complex Systems, AUTOMATA 2017, Lecture Notes in Computer Science, 10248 (2017), Springer, Cham,
Analogamente a quanto fatto in Pattern-avoiding Dyck paths (con Antonio Bernini, Renzo Pinzani e Julian West), Discrete Mathematics and Theoretical Computer Science Proceedings, AS (2013) 713-724, la nozione di pattern di un cammino di Schröder viene studiata da un punto di vista enumerativo. Specificamente, vengono ricavate formule per il numero dei cammini di Schröder che coprono/sono coperti da un fissato cammino (in termini di parametri naturali sui cammini) e vengono enumerate alcune classi di cammini di Schröder che evitano un fissato cammino.

Progetti di ricerca

 

Metodo ECO

Si tratta di un metodo di combinatoria enumerativa e biiettiva sviluppato da un gruppo di ricercatori del dipartimento di Sistemi e Informatica dell'Università di Firenze agli inizi degli anni '90 (comprendente Renzo Pinzani, Elena Barcucci, Alberto Del Lungo ed Elisa Pergola). Data una classe di oggetti combinatoria e un concetto di taglia definito per tale classe, il metodo ECO consente di costruire, a partire da un oggetto di taglia n, un insieme di oggetti di taglia n+1, in modo tale che oggetti diversi possiedono uno ed un solo padre. In tal modo si viene a generare una partizione degli oggetti di taglia n, per ogni n. La costruzione descritta può spesso essere descritta mediante un'opportuna regola di successione, il che in diverse circostanze dà la possibilità di enumerare la classe in oggetto secondo svariati parametri.

A linear operator approach to succession rules (con Renzo Pinzani), Linear Algebra and Its Applications, 348 (2002) 231-246.
Ogni regola di successione viene rappresentata mediante un opportuno operatore lineare (detto rule operator) nello spazio vettoriale dei polinomi in una variabile, e tutte le informazioni enumerative contenute nella regola vengono ritrovate in tale operatore. Vengono considerati diversi esempi, e viene mostrata l'utilità di tale approccio nella determinazione di una forma standard per una data regola di successione.

An algebraic characterization of the set of succession rules (con Elisa Pergola, Renzo Pinzani e Simone Rinaldi, Theoretical Computer Science, 281 (2002) 351-367.
Viene definita un'algebra delle regole di successione in modo tale che, date due regole di successione, viene stabilita la forma di una regola di successione la cui sequenza numerica associata è legata alle sequenze numeriche associate alle regole di successione di partenza tramite l'applicazione di svariate operazioni algebriche (quali somma, prodotto di convoluzione, prodotto di Hadamard, ecc.). Nella dimostrazione di quasi tutti i teoremi si rivela estremamente utile il metodo dei rule operators.

Jumping succession rules and their generating functions (con Elisa Pergola, Renzo Pinzani e Simone Rinaldi), Discrete Mathematics, 271 (2003) 29-50.
Si definisce il concetto di regola di successione con salto: si tratta di una regola di successione nel cui albero di generazione ogni nodo produce figli non soltanto al livello successivo dell'albero, bensì produce insiemi di figli a diversi livelli successivi. Viene analizzata la situazione in cui gli insiemi di figli prodotti ai vari livelli sono tutti descritti dalla medesima regola di successione, e vengono forniti risultati enumerativi completi (cioè la sequenza numerica della regola con salto viene espressa in funzione della sequenza numerica associata alla regola di successione che descrive la produzione di ogni insieme di figli nell'albero di generazione).

Enumerative results on integer partitions using the ECO method (con Renzo Pinzani e Simone Rinaldi), Mathematics and Computer Science, III (Wien, 2004), Trends in Mathematics, Birkhauser, Basel, pp.25-36.
Viene definita una regola di successione con infiniti salti per le partizioni dei numeri interi. Vengono espressi alcuni risultati classici usando tale regola di successione. Le possibili applicazioni originali riguardano le lecture hall partitions (per le quali viene congetturata una possibile nuova dimostrazione biiettiva del teorema fondamentale che le mette in relazione con le partizioni in un numero finito di parti dispari) e le partizioni contenute in un uncino generalizzato (per esse viene fornito anche un risultato enumerativo completo).

Production matrices (con Emeric Deutsch e Simone Rinaldi, Advances in Applied Mathematics, 34 (2005) 101-122.
Viene definito il concetto di matrice di produzione, che è il corrispettivo matriciale della nozione di rule operator. Come nel caso dei rule operator, viene spiegato come leggere nella matrice di produzione tutte le principali informazioni enumerative contenute nella regola di successione. Vengono inoltre definite opportune operazioni sulle matrici di produzione corrispondenti a numerose operazioni algebriche sulle sequenze numeriche determinate dalle regole di successione associate.

Enumerating permutations avoiding three Babson-Steingrimsson patterns (con Antonio Bernini e Renzo Pinzani), Annals of Combinatorics, 9 (2005) 137-162.
Il metodo ECO e una particolare rappresentazione grafica delle permutazioni vengono utilizzati per enumerare tutte le classi di permutazioni che evitano simultaneamente tre motivi generalizzati di lunghezza 3 di tipo a-bc oppure ab-c, confermando in tal modo una serie di congetture di Claesson e Mansour.

Catalan-like numbers and succession rules (con Renzo Pinzani), Pure Mathematics and Applications, 16 (2005) 229-250.
Viene definita una trasformazione lineare biiettiva che, in numerosissimi casi, trasforma una matrice ECO (vale a dire la matrice infinita associata ad un albero di generazione in modo tale che l'elemento di posto (n,k) rappresenta il numero di etichette (k) a livello (n)) in una matrice di Aigner i cui Catalan-like numbers associati coincidono con la sequenza numerica determinata dalla matrice ECO di partenza. Vengono forniti diversi esempi e vengono analizzate alcune classi speciali di regole di successione (regole fattoriali e regole differenziali).

Some statistics on permutations avoiding generalized patterns (con Antonio Bernini e Mathilde Bouvel), Pure Mathematics and Applications, 18 (2007) 223-237.
Vengono studiate le statistiche "primo/ultimo elemento" in alcune classi di permutazioni a motivo escluso.

Production matrices and Riordan arrays (con Emeric Deutsch e Simone Rinaldi), Annals of Combinatorics, 13 (2009) 65-85.
Vengono stabiliti i rapporti fra matrici ECO e Riordan arrays; in particolare, viene stabilita qual'è la forma delle matrici di produzione le cui matrici ECO associate sono Riordan array o Riordan array esponenziali. Vengono inoltre studiate alcune proprietà di matrici di produzione associate a regole di successione finite e razionali. Il lavoro è corredato da una vasta galleria di esempi.

Enumeration of some classes of words avoiding two generalized patterns of length three (con Antonio Bernini e Renzo Pinzani), Journal of Automata, Languages and Combinatorics, 14 (2009) 129-147.
Il metodo utilizzato in Enumerating permutations avoiding three Babson-Steingrimsson patterns (con Antonio Bernini e Renzo Pinzani), Annals of Combinatorics, 9 (2005) 137-162 per contare permutazioni a motivo escluso viene qui ripreso e adattato al caso delle parole. Come applicazione di tale metodo, vengono enumerate diverse classi di parole che escludono simultaneamente due motivi generalizzati di lunghezza 3.

Mixed succession rules: the commutative case (con Silvia Bacchelli, Renzo Pinzani e Renzo Sprugnoli), Journal of Combinatorial Theory, Series A, 117 (2010) 568-582.
Generalizzando ciò che è stato fatto in Jumping succession rules and their generating functions (con Elisa Pergola, Renzo Pinzani e Simone Rinaldi), Discrete Mathematics, 271 (2003) 29-50, vengono studiate regole di successione nel cui albero di generazione i nodi possono produrre figli a più livelli sottostanti e in accordo a diverse regole di produzione. Il caso in cui i rule operators associati alle regole di successione commutano è studiato in dettaglio, e viene ricavata una formula generale per esprimere la sequenza numerica associata ad una regola doppia (in cui un nodo a livello n dell'albero di generazione produce un set di figli a livello n+1 in accordo a una certa regola di produzione e un set di figli a livello n+2 in accordo a un'altra, eventualmente diversa, regola di produzione) in termini di parametri enumerativi delle due regole componenti. Alcuni esempi e interpretazioni combinatorie vengono forniti a supporto della teoria sviluppata.

ECO species (con Pierre Leroux), Séminaire Lotharingien de Combinatoire 61A (2010) Article B61Al, 23pp.
Viene introdotto il concetto di specie ECO per descrivere formalmente, all'interno della teoria delle specie (lineari), i concetti di costruzione ECO e di albero di generazione. Vengono poi descritte e illustrate tramite esempi alcune operazioni sulle specie ECO.

Some applications arising from the interactions between the theory of Catalan-like numbers and the ECO method (con Elisa Pergola, Renzo Pinzani e Simone Rinaldi), Ars Combinatoria, 99 (2011) 109-128.
Vengono descritte alcune applicazioni combinatorie derivanti dall'utilizzo della trasformazione lineare che connette matrici ECO con matrici di Aigner introdotta in Catalan-like numbers and succession rules. La possibilità di passare da una teoria all'altra, infatti, consente di affrontare problemi ostici in una delle due semplicemente traducendoli nell'altra. Con questa tecnica, è stata definita una biiezione fra cammini di Grand-Dyck che iniziano con un passo ascendente e cammini di Motzkin con passi orizzontali bicolorati, eccetto che sull'asse delle x, ove possono assumere 3 diversi colori. Inoltre, la stessa tecnica ha permesso di fornire un'interpretazione combinatoria per una matrice di Aigner particolarmente ostica, mediante una classe di poliomini steep colorati di tipo speciale. 

Progetti di ricerca

 

Combinatoria enumerativa e biiettiva

Some bijective results about the area of Schröder paths (con Elisabetta Grazzini, Elisa Pergola e Simone Rinaldi), Theoretical Computer Science, 307 (2003) 327-335.
Viene fornita un'interpretazione combinatoria dei termini di indice pari della sequenza 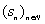definita dalla relazione di ricorrenza 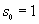, , 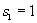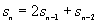in termini di area totale dei cammini di Schröder elevati.

Enumeration of generalized hook partitions (con Simone Rinaldi), Integers, 5 (2005) #A29 (7 pp.).
Viene determinata la funzione generatrice della classe delle partizioni di interi il cui diagramma di Ferrers è contenuto in un uncino generalizzato oppure nell'intersezione di due uncini generalizzati (un uncino generalizzato differisce da un uncino classico per il fatto che l'altezza e la larghezza dell'uncino sono interi positivi non necessariamente uguali a 1).

Combinatorial properties of Catalan pairs (con Filippo Disanto, Renzo Pinzani e Simone Rinaldi), Electronic Notes in Discrete Mathematics, 34 (2009) 429-433.
Catalan pairs: a relational-theoretic approach to Catalan numbers (con Filippo Disanto, Renzo Pinzani e Simone Rinaldi), versione estesa, Advances in Applied Mathematics, 45 (2010) 505-517.
Viene introdotta la nozione di coppia di Catalan (R,S) (ove R e S sono relazioni di ordine parziale stretto su uno stesso insieme con determinate proprietà), con lo scopo di fornire un linguaggio comune a molte interpretazioni combinatorie dei numeri di Catalan. Dopo aver dimostrato alcune proprietà fondamentali delle coppie di Catalan, fra cui il fatto che, a meno di isomorfismi, esse sono contate dai numeri di Catalan, vengono proposti alcuni esempi di interpretazioni dei numeri di Catalan per le quali è abbastanza facile determinare la coppia di Catalan associata. Successivamente vengono studiati gli insiemi parzialmente ordinati associati a R e S, mostrando in particolare che la relazione R determina univocamente la coppia di Catalan e che l'insieme parzialmente ordinato associato a R può essere descritto in termini di configurazioni escluse. Vengono infine descritte le coppie di Catalan per le quali R possiede determinate proprietà (i.e. determina un insieme parzialmente ordinato connesso, oppure un reticolo, oppure un reticolo distributivo) e viene leggermente modificata la definizione di coppia di Catalan con lo scopo di definire un analogo concetto per altre sequenze intere, quali coefficienti binomiali centrali e numeri di Schröder.

On the enumeration of d-minimal permutations (con Mathilde Bouvel), Discrete Mathematics and Theoretical Computer Science, 15(2) (2013) 33-48.
Viene suggerito un possibile approccio allo studio (e in particolare all'enumerazione) delle permutazioni minimali con d discese utilizzando una famiglia di tableaux di Young sghembi. Tale approccio consente di dedurre una formula generale in termini di somme di determinanti. Viene poi proposta anche un'estensione della famiglia di tableaux di cui sopra, che conduce, fra le altre cose, ai numeri Euleriani e ad alcune presumibilmente nuove loro proprietà.

Schröder partitions and Schröder tableaux, in: Lipták Z., Smyth W. (eds) Combinatorial Algorithms. Lecture Notes in Computer Science, 9538 (2016), Springer, Cham, pp. 161-172.
Schröder partitions, Schröder tableaux and weak poset patterns, versione estesa, sottomesso (2016).
Vengono introdotte le nozioni di diagramma di Schröder e di tableau di Schröder, allo scopo di fornire una sorta di analogo delle classiche nozioni di diagramma di Young e di tableau di Young. Dopo aver studiato alcune semplici proprietà dell'insieme parzialmente ordinato dei diagrammi di Schröder, viene definito un algoritmo analogo alla corrispondenza di Robinson-Schensted per tableaux di Young standard e ne vengono studiate alcune proprietà. Infine, i tableau di Schröder vengono messi in relazione con gli interval order tramite la poco nota nozione di motivo debole di un poset.

Progetti di ricerca

 

 

Altri progetti di ricerca