Schedule:

11:00-13:00, Monday 06/06 through Friday 10/06.

 

Abstract:

In this course we present the fundamental elements of the theory of slice regular functions on a real alternative ∗-algebra A. This function theory generalizes to higher dimensions the classical theory of holomorphic functions of a complex variable.

When A is the algebra of quaternions or the algebra of octonions, the theory extends the one of Cullen regular functions introduced by Gentili and Struppa in 2006/07. If A is the Clifford algebra R_n with signature (0,n), slice regular functions will be defined on a proper subset of R_n , what we call the quadratic cone of the algebra. In particular, by restricting the Clifford variables to the subspace R^{n+1} of paravectors, we get the theory of slice monogenic functions introduced by Colombo, Sabadini and Struppa in 2009.

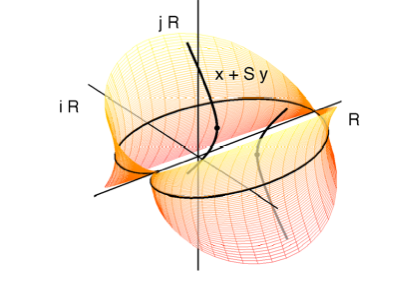
The slice character of the definition of regularity comes from a basic property of the quadratic cone of A: it decomposes as a union of copies of the complex plane, with the property that any two such copies have the real line (the scalar multiples of the unity of A) as intersection.

Among the results that our approach allows to obtain there is a fundamental theorem of algebra for polynomials with coefficients in A and a Cauchy integral formula for slice functions of class C^1. Other developments of the theory and future lines of research will be addressed.​