Quaternionic linear operators and their functional calculus
Schedule:
14:00-16:00 on Monday 04/07,
9:00-11:00 and 14:00-16:00 on Tuesday 05/07 and Wednesday 06/07.
Abstract:
Holomorphic functions play an important role in operator theory because they allow to define functions of linear operators which include, for example, the evolution operator and the fractional powers of operators. In this course we shall study an analog theory for quaternionic linear operators.
The interest in quaternionic linear operators is motivated by a celebrated paper of Birkhoff and von Neumann who showed, in 1936, that the Schrödinger equation can be formulated only in the complex or quaternionic setting.
In quaternionic operator theory the notion of slice regularity (or slice hyperholomorphicity) replaces the notion of holomorphicity and it allows to define functions of quaternionic linear operators. In fact, given a slice regular function f and a quaternionic linear operator T the map f→f(T) is called quaternionic functional calculus.
The Cauchy formula of slice hyperholomorphic functions suggests that the calculus is based on a new notion of spectrum, the so-called S-spectrum, which involves a second order operator.
In this course we will study quaternionic linear operators, Hilbert and Banach spaces over the quaternions, the S-spectrum, and the main properties of the quaternionic functional calculus.

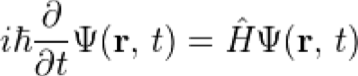
< previous
home >